•Tehtävä 1

In[1]:=

lauseke = x y/(x^2 + y^2) ;

In[2]:=

lauseke /. {x -> 2, y -> 3}

Out[2]=

6/13

In[3]:=

lauseke /. {x -> -5, y -> Pi}

Out[3]=

-(5 π)/(25 + π^2)

In[4]:=

N[lauseke /. {x -> 2, y -> 3}, 50]

Out[4]=

0.46153846153846153846153846153846153846153846153846153846153846`50

In[5]:=

N[lauseke /. {x -> -5, y -> Pi}, 50]

Out[5]=

-0.4504772433683886280241556227820658981065104939750286652713318686397`50

•Tehtävä 2

In[6]:=

yhtaloa = 168 x == 195

Out[6]=

168 x == 195

In[7]:=

ratkaisua = Solve[yhtaloa, x]

Out[7]=

{{x -> 65/56}}

In[8]:=

yhtaloa /. ratkaisua

Out[8]=

{True}

In[9]:=

yhtalob = x^2 - 2 x - 4 == 0

Out[9]=

-4 - 2 x + x^2 == 0

In[10]:=

ratkaisub = Solve[yhtalob, x]

Out[10]=

{{x -> 1 - 5^(1/2)}, {x -> 1 + 5^(1/2)}}

In[11]:=

yhtalob /. ratkaisub // Simplify

... 999986` was reached. Increasing the value of $MaxExtraPrecision may help resolve the uncertainty.

... 999986` was reached. Increasing the value of $MaxExtraPrecision may help resolve the uncertainty.

Out[11]=

{True, True}

Tässä kuten muutamissa myöhemmissäkin kohdissa tulee kummallisia $MaxExtraPrecision-virheilmoituksia. Oikeastaan tällaisia ei pitäisi tulla, koska juurilausekkeiden sieventäminen on puhtaasti algebrallista eikä siinä pitäisi laskentatarkkuudella olla merkitystä. Tarkempaa tietoa Help Browserista hakusanoilla $MaxExtraPrecision ja $MaxExtraPrecision::meprec. Hämäräksi kuitenkin jää, miksi Mathematica tässä kohden antaa tällaisia ilmoituksia.

In[12]:=

yhtaloc = x^3 - x^2 + x - 21 == 0

Out[12]=

-21 + x - x^2 + x^3 == 0

In[13]:=

ratkaisuc = Solve[yhtaloc, x]

Out[13]=

{{x -> 3}, {x -> -1 - i 6^(1/2)}, {x -> -1 + i 6^(1/2)}}

In[14]:=

yhtaloc /. ratkaisuc // Simplify

... 999986` was reached. Increasing the value of $MaxExtraPrecision may help resolve the uncertainty.

... 999986` was reached. Increasing the value of $MaxExtraPrecision may help resolve the uncertainty.

Out[14]=

{True, True, True}

In[15]:=

yhtalod = (a - b) x^2 + a x + b == 0

Out[15]=

b + a x + (a - b) x^2 == 0

In[16]:=

ratkaisud = Solve[yhtalod, x]

Out[16]=

{{x -> -1}, {x -> b/(-a + b)}}

In[17]:=

yhtalod /. ratkaisud // Simplify

Out[17]=

{True, True}

•Tehtävä 3

In[18]:=

ratkaisu = Solve[a x^2 + b x + c == 0, x]

Out[18]=

{{x -> (-b - (b^2 - 4 a c)^(1/2))/(2 a)}, {x -> (-b + (b^2 - 4 a c)^(1/2))/(2 a)}}

In[19]:=

{ratk1, ratk2} = x /. ratkaisu

Out[19]=

{(-b - (b^2 - 4 a c)^(1/2))/(2 a), (-b + (b^2 - 4 a c)^(1/2))/(2 a)}

In[20]:=

tulos = ratk1^2 + ratk1 ratk2 + ratk2^2 // Simplify

Out[20]=

(b^2 - a c)/a^2

In[21]:=

ratkaisu /. {a -> 2, b -> 3, c -> 4}

Out[21]=

{{x -> 1/4 (-3 - i 23^(1/2))}, {x -> 1/4 (-3 + i 23^(1/2))}}

In[22]:=

tulos /. {a -> 2, b -> 3, c -> 4}

Out[22]=

1/4

•Tehtävä 4

In[23]:=

ratkaisu = Solve[{3 x - 2 y == 1, 4 x + 5 y == 2}, {x, y}]

Out[23]=

{{x -> 9/23, y -> 2/23}}

•Tehävä 5

In[24]:=

Plot[{Log[x^2 + 1], Sqrt[x + 1]}, {x, -0.99, 10}] ;

[Graphics:HTMLFiles/ratk2_51.gif]

In[25]:=

Plot[{Log[x^2 + 1], Sqrt[x + 1]}, {x, 10, 100}] ;

[Graphics:HTMLFiles/ratk2_53.gif]

Näyttäisi tulevan 3 juurta. Enempää ei ole, sillä funktiot ovat suurillan x:n arvoilla likimain 2 ln x ja x^(1/2). Logaritmi taas kasvaa hitaammin kuin mikä tahansa positiivinen potenssi. Täsmällisempi analyysi derivaatoilla!

In[26]:=

FindRoot[Log[x^2 + 1] == Sqrt[x + 1], {x, -0.9}]

Out[26]=

{x -> -0.7769493284354522`}

In[27]:=

FindRoot[Log[x^2 + 1] == Sqrt[x + 1], {x, 2}]

Out[27]=

{x -> 2.251405748381093`}

In[28]:=

FindRoot[Log[x^2 + 1] == Sqrt[x + 1], {x, 50}]

Out[28]=

{x -> 72.30968099266737`}

•Tehtävä 6

In[29]:=

Needs["Graphics`ImplicitPlot`"]

In[30]:=

ImplicitPlot[{Exp[x] + Sin[y] == 0, x^6 - x y + y^6 == 4}, {x, -2, 2}, {y, -2, 2}]

[Graphics:HTMLFiles/ratk2_65.gif]

Out[30]=

-Graphics -

Siis 2 juurta näyttää ainakin löytyvän. Määrätään ne. Itse asiassa muita ratkaisuja ei voi olla, sillä jos x>0, niin ensimmäisellä yhtälöllä ei ole ratkaisua ja jos Abs(x)>2, niin toisella yhtälöllä ei ole ratkaisua, kuten tarkemmalla analyysilla voidaan osoittaa.

In[31]:=

FindRoot[{Exp[x] + Sin[y] == 0, x^6 - x y + y^6 == 4}, {x, 0}, {y, -1.5}]

Out[31]=

{x -> -0.048107777947176106`, y -> -1.2630909799481025`}

In[32]:=

FindRoot[{Exp[x] + Sin[y] == 0, x^6 - x y + y^6 == 4}, {x, -1.5}, {y, -0.5}]

Out[32]=

{x -> -1.2781623581523698`, y -> -0.28228267200810625`}

•Tehtävä 7

In[33]:=

p = x^3 - 2 x - 5

Out[33]=

-5 - 2 x + x^3

In[34]:=

ratkaisu = Solve[p == 0, x]

Out[34]=

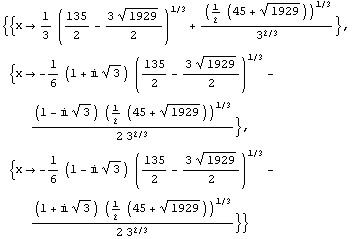
{{x -> 1/3 (135/2 - (3 1929^(1/2))/2)^(1/3) + (1/2 (45 + 1929^(1/2)))^(1/3)/3^(2/3)}, {x -& ... ) (135/2 - (3 1929^(1/2))/2)^(1/3) - ((1 + i 3^(1/2)) (1/2 (45 + 1929^(1/2)))^(1/3))/(2 3^(2/3))}}

In[35]:=

p == 0 /. ratkaisu // Simplify

$MaxExtraPrecision :: meprec : In increasing internal precision while attempting to evaluate ... 999986` was reached. Increasing the value of $MaxExtraPrecision may help resolve the uncertainty.

... 2 2 2 << 1 >> << 1 >>

... 2 2 2 << 1 >> << 1 >>

General :: stop : Further output of $MaxExtraPrecision :: \" meprec \" will be suppressed during this calculation.

Out[35]=

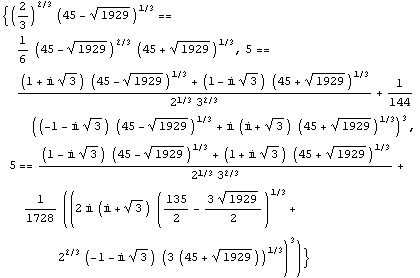
{(2/3)^(2/3) (45 - 1929^(1/2))^(1/3) == 1/6 (45 - 1929^(1/2))^(2/3) (45 + 1929^(1/2))^(1/3), 5 ... 1/2)) (135/2 - (3 1929^(1/2))/2)^(1/3) + 2^(2/3) (-1 - i 3^(1/2)) (3 (45 + 1929^(1/2)))^(1/3))^3)}

Ei siis sieventynyt.

In[36]:=

p /. ratkaisu // Simplify

Out[36]=

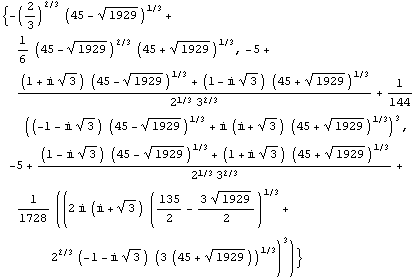
{-(2/3)^(2/3) (45 - 1929^(1/2))^(1/3) + 1/6 (45 - 1929^(1/2))^(2/3) (45 + 1929^(1/2))^(1/3), - ... 1/2)) (135/2 - (3 1929^(1/2))/2)^(1/3) + 2^(2/3) (-1 - i 3^(1/2)) (3 (45 + 1929^(1/2)))^(1/3))^3)}

Ei taida sieventyä. Otetaan edellisestä likiarvo:

In[37]:=

p /. ratkaisu // N

Out[37]=

{3.552713678800501`*^-15, -5.329070518200751`*^-15 + 3.1086244689504383`*^-15 i, -5.329070518200751`*^-15 - 3.1086244689504383`*^-15 i}

Numeerinen ratkaisu:

In[38]:=

numratk = NSolve[p == 0, x]

Out[38]=

{{x -> -1.0472757407711633` - 1.1359398890889278` i}, {x -> -1.0472757407711633` + 1.1359398890889278` i}, {x -> 2.0945514815423265`}}

In[39]:=

p == 0 /. numratk

Out[39]=

{False, False, False}

In[40]:=

p /. numratk

Out[40]=

{-2.6645352591003757`*^-15 - 4.440892098500626`*^-16 i, -2.6645352591003757`*^-15 + 4.440892098500626`*^-16 i, -1.7763568394002505`*^-15}

•Tehtävä 8

In[41]:=

ratkaisu = Solve[Abs[x - 1] + Abs[x - 3] == 3, x]

Solve :: ifun : Inverse functions are being used by Solve , so some solutions may not be found.

Out[41]=

{{x -> 1/2}, {x -> 7/2}}

Siis varoitus, että joku ratkaisu voi puuttua. Piirretään kuvaaja.

In[42]:=

Plot[{Abs[x - 1] + Abs[x - 3] - 3}, {x, -10, 10}]

[Graphics:HTMLFiles/ratk2_95.gif]

Out[42]=

-Graphics -

Siis kaikki ratkaisut löytyivät, kun käytetään hyväksi tietoa, että kuvaaja paloittain suora.

Tietenkin voitaisiin poistaa itseisarvomerkit (myös määrittelyalueista väittämättä) ja ratkaista saadut yhtälöparit ja lopuksi testata mitkä ratkaisuista toteuttavat alkuperäisen yhtälön. Voisimme myös suorittaa neliöön korotuksen ja ratkaista saadun yhtälön ja sitten tarkastaa, ovatko saadut ratkaisut alkuperäisen yhtälön ratkaisuja.

•Tehtävä 9

In[43]:=

likiarvo = (n + 1/2) Log[n] - n + Log[Sqrt[2 Pi]]

Out[43]=

-n + (1/2 + n) Log[n] + 1/2 Log[2 π]

In[44]:=

virhe = Log[n !] - likiarvo

Out[44]=

n - (1/2 + n) Log[n] - 1/2 Log[2 π] + Log[n !]

In[45]:=

suhtvirhe = virhe/Log[n !]

Out[45]=

(n - (1/2 + n) Log[n] - 1/2 Log[2 π] + Log[n !])/Log[n !]

In[46]:=

virhe /. {n -> 10} // N

Out[46]=

0.008330563433360805`

In[47]:=

virhe /. {n -> 100} // N

Out[47]=

0.0008333305555452419`

In[48]:=

virhe /. {n -> 1000} // N

Out[48]=

0.00008333333065868587`

In[49]:=

suhtvirhe /. {n -> 10} // N

Out[49]=

0.0005515317721266773`

In[50]:=

suhtvirhe /. {n -> 100} // N

Out[50]=

2.2910100240658315`*^-6

In[51]:=

suhtvirhe /. {n -> 1000} // N

Out[51]=

1.4095318664081416`*^-8

•Tehtävä 10

In[52]:=

Needs["Graphics`ImplicitPlot`"]

In[53]:=

yht1 = 16 x^2 + 9 y^2 + 24 x y - 170 x + 310 y - 465 == 0

Out[53]=

-465 - 170 x + 16 x^2 + 310 y + 24 x y + 9 y^2 == 0

In[54]:=

yht2 = 5 x^2 + 8 y^2 + 4 x y - 32 x - 56 y + 80 == 0

Out[54]=

80 - 32 x + 5 x^2 - 56 y + 4 x y + 8 y^2 == 0

In[55]:=

ImplicitPlot[{yht1, yht2}, {x, -2, 7}, {y, 0, 7}]

[Graphics:HTMLFiles/ratk2_121.gif]

Out[55]=

-Graphics -

Haetaan kuvaajan perusteella leikkauspisteille likiarvoja. Kuvaajan perusteella toinen käyristä on ellipsi, joten ratkaisuja ei ole piirtoalueen ulkopuolella; eli niitä on 2.

In[56]:=

FindRoot[{yht1, yht2}, {x, 0}, {y, 2}]

Out[56]=

{x -> 0.457005241759929`, y -> 1.6078899953650685`}

In[57]:=

FindRoot[{yht1, yht2}, {x, 5}, {y, 2}]

Out[57]=

{x -> 4.809962514073391`, y -> 2.0555129838120543`}

Yritetään sitten ratkaista tarkasti. Tulee hankalan näköinen vastaus.

In[58]:=

Solve[{yht1, yht2}, {x, y}]

Out[58]=

{{x -> 1/12755178 (1879717874/5 - 6232862 √ (579272/9375 + 1/46875 ((1938532197165936 ... (1/3)) + 1/46875 (4 2^(2/3) (757239139517944039 + 637875 3425277286028853209865^(1/2))^(1/3)))))}}

Lasketaan likiarvot, jolloin nähdään, että reaaliset ratkaisut ovat samoja kuin edellä.

In[59]:=

% // N

Out[59]=

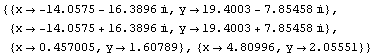
{{x -> -14.057483877908293` - 16.38959369741863` i, y -> 19.4002985104123` - 7.85457651 ... 417597401`, y -> 1.607889995365049`}, {x -> 4.809962514056828`, y -> 2.055512983810356`}}

Myös NSolve toimisi:

In[60]:=

NSolve[{yht1, yht2}, {x, y}]

Out[60]=

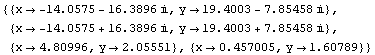
{{x -> -14.057483877908403` - 16.38959369741868` i, y -> 19.40029851041234` - 7.8545765 ... 4056654`, y -> 2.055512983810338`}, {x -> 0.45700524175993856`, y -> 1.607889995365069`}}

Converted by Mathematica  (August 21, 2003)