•Tehtävä 1

In[1]:=

trooppvuosi = 45 + 48 * 60 + 5 * 60 * 60 + 365 * 24 * 60 * 60

Out[1]=

31556925

In[2]:=

pyoraika = 4 + 56 * 60 + 23 * 60 * 60

Out[2]=

86164

In[3]:=

pyorlukum = trooppvuosi/pyoraika

Out[3]=

31556925/86164

In[4]:=

pyorlukum // N

Out[4]=

366.2425723039785`

kuten tietenkin pitääkin.

•Tehtävä 2

In[5]:=

Sqrt[7 - 4 Sqrt[3]] // Simplify

Out[5]=

(7 - 4 3^(1/2))^(1/2)

In[6]:=

Sqrt[7 - 4 Sqrt[3]] // FullSimplify

Out[6]=

2 - 3^(1/2)

Simplify ei siis tehoa, mutta FullSimplify tehoaa.

•Tehtävä 3

In[7]:=

poly = x^5 + 2 x^4 y - x^3 y^2 - 2 x^2 y^3 - x^3 y - 2 x^2 y^2 + x y^3 + 2 y^4

Out[7]=

x^5 - x^3 y + 2 x^4 y - 2 x^2 y^2 - x^3 y^2 + x y^3 - 2 x^2 y^3 + 2 y^4

In[8]:=

tekijat = poly // Factor

Out[8]=

(x - y) (x^2 - y) (x + y) (x + 2 y)

In[9]:=

poly2 = tekijat // Expand

Out[9]=

x^5 - x^3 y + 2 x^4 y - 2 x^2 y^2 - x^3 y^2 + x y^3 - 2 x^2 y^3 + 2 y^4

In[10]:=

poly == poly2

Out[10]=

True

Päädyttiin siis takaisin samaan lausekkeeseen, kuten tietenkin pitääkin.

•Tehtävä 4

In[11]:=

a = 5.27

Out[11]=

5.27`

In[12]:=

b = 3.16

Out[12]=

3.16`

In[13]:=

cc = 72 + 50/60

Out[13]=

437/6

Kosinilause:

In[14]:=

etaisyys = Sqrt[a^2 + b^2 - 2 a b Cos[cc Degree]]

Out[14]=

5.284698797478515`

•Tehtävä 5

Funktiot:

In[15]:=

f1 = x^n

Out[15]=

x^n

In[16]:=

f2 = x^x

Out[16]=

x^x

In[17]:=

f3 = Sin[x]^4 + Cos[x]^4

Out[17]=

Cos[x]^4 + Sin[x]^4

Derivaatat:

In[18]:=

d1 = D[f1, x]

Out[18]=

n x^(-1 + n)

In[19]:=

d2 = D[f2, x]

Out[19]=

x^x (1 + Log[x])

In[20]:=

d3 = D[f3, x]

Out[20]=

-4 Cos[x]^3 Sin[x] + 4 Cos[x] Sin[x]^3

Integraalit:

In[21]:=

i1 = Integrate[d1, x]

Out[21]=

x^n

In[22]:=

i2 = Integrate[d2, x]

Out[22]=

x^x

Kahdessa ensimmäisessä tapauksessa palataan samaan mistä lähdettiin, kolmannessa ei:

In[23]:=

i3 = Integrate[d3, x]

Out[23]=

1/4 Cos[4 x]

In[24]:=

f3 - i3 // Simplify

Out[24]=

3/4

Ja saahan se toki nollasta eroava vakio ollakin.

•Tehtävä 6

In[25]:=

lsk = (x - 1)/(1 - 1/Sqrt[x])/(1 + 1/Sqrt[x])

Out[25]=

(-1 + x)/((1 - 1/x^(1/2)) (1 + 1/x^(1/2)))

In[26]:=

lsk // Simplify

Out[26]=

x

•Tehtävä 7

In[27]:=

a = Random[Integer, {1, 100}]

Out[27]=

98

In[28]:=

b := Random[Integer, {1, 100}]

In[29]:=

Table[a, {10}]

Out[29]=

{98, 98, 98, 98, 98, 98, 98, 98, 98, 98}

In[30]:=

Table[b, {10}]

Out[30]=

{24, 69, 92, 32, 14, 47, 74, 9, 61, 28}

Edellisessä tapauksessa lauseke lasketaan heti. Jälkimmäisessä määritellään, mitä b on, ja tätä määritelmää käytetään aina, kun b halutaan laskea.

•Tehtävä 8

Funktiot:

In[31]:=

f1 = Sin[3 x]

Out[31]=

Sin[3 x]

In[32]:=

f2 = Cos[7 x]

Out[32]=

Cos[7 x]

In[33]:=

f3 = Sin[x]^6

Out[33]=

Sin[x]^6

In[34]:=

f4 = Cos[x]^11

Out[34]=

Cos[x]^11

Eri sievennyskomennot sovellettuina kaikkiin:

In[35]:=

{f1, f2, f3, f4} // TrigFactor

Out[35]=

{(1 + 2 Cos[2 x]) Sin[x], Cos[x] (-1 + 2 Cos[2 x] - 2 Cos[4 x] + 2 Cos[6 x]), Sin[x]^6, Cos[x]^11}

In[36]:=

{f1, f2, f3, f4} // TrigExpand

Out[36]=

{3 Cos[x]^2 Sin[x] - Sin[x]^3, Cos[x]^7 - 21 Cos[x]^5 Sin[x]^2 + 35 Cos[x]^3 Sin[x]^4 - 7 Cos[x] Sin[x]^6, Sin[x]^6, Cos[x]^11}

In[37]:=

{f1, f2, f3, f4} // TrigReduce

Out[37]=

{Sin[3 x], Cos[7 x], 1/32 (10 - 15 Cos[2 x] + 6 Cos[4 x] - Cos[6 x]), 1/1024 (462 Cos[x] + 330 Cos[3 x] + 165 Cos[5 x] + 55 Cos[7 x] + 11 Cos[9 x] + Cos[11 x])}

In[38]:=

{f1, f2, f3, f4} // TrigToExp

Out[38]=

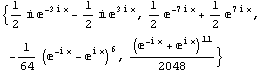
{1/2 i e^(-3 i x) - 1/2 i e^(3 i x), 1/2 e^(-7 i x) + 1/2 e^(7 i x), -1/64 (e^(-i x) - e^(i x))^6, (e^(-i x) + e^(i x))^11/2048}

In[39]:=

% // ExpToTrig

Out[39]=

{Sin[3 x], Cos[7 x], Sin[x]^6, Cos[x]^11}

TrigToExp ja ExpToTrig ovat toistensa käänteisfunktioita. Näiden avulla voidaan trigonometriset funktiot lausua komplksisen eksponenttifunktion avulla ja kääntäen.

•Tehtävä 9

In[40]:=

f1 = x/(x^2 + 5 x + 6)

Out[40]=

x/(6 + 5 x + x^2)

In[41]:=

f2 = (2 x + 7)/(x^3 + 3 x^2 + 3 x + 1)

Out[41]=

(7 + 2 x)/(1 + 3 x + 3 x^2 + x^3)

In[42]:=

os1 = Apart[f1]

Out[42]=

-2/(2 + x) + 3/(3 + x)

In[43]:=

os2 = Apart[f2]

Out[43]=

5/(1 + x)^3 + 2/(1 + x)^2

In[44]:=

os1 // Together // ExpandAll

Out[44]=

x/(6 + 5 x + x^2)

In[45]:=

os2 // Together // ExpandAll // Together

Out[45]=

(7 + 2 x)/(1 + 3 x + 3 x^2 + x^3)

•Tehtävä 10

In[46]:=

f1 = (x + 1)/(x^2 - x + 1)^10

Out[46]=

(1 + x)/(1 - x + x^2)^10

In[47]:=

f2 = Log[1 + x^12]

Out[47]=

Log[1 + x^12]

In[48]:=

i1 = Integrate[f1, x]

Out[48]=

(-1 + x)/(9 (1 - x + x^2)^9) + (17 (-1 + 2 x))/(216 (1 - x + x^2)^8) + (85 (-1 + 2 x))/(756 (1 ... )^2) + (12155 (-1 + 2 x))/(6561 (1 - x + x^2)) + (48620 ArcTan[(-1 + 2 x)/3^(1/2)])/(6561 3^(1/2))

In[49]:=

i2 = Integrate[f2, x]

Out[49]=

-12 x + 2^(1/2) ArcTan[(-2^(1/2) + 2 x)/2^(1/2)] + 2^(1/2) ArcTan[(2^(1/2) + 2 x)/2^(1/2)] + ( ... (2 2^(1/2)) + ((1 + 3^(1/2)) Log[2 + 2^(1/2) x + 6^(1/2) x + 2 x^2])/(2 2^(1/2)) + x Log[1 + x^12]

In[50]:=

D[i1, x] == f1 // Simplify

Out[50]=

True

In[51]:=

D[i2, x] == f2 // Simplify

Out[51]=

True

Converted by Mathematica  (August 16, 2003)