Simo K. Kivelä / 05.05.2003

Yhtälöiden ratkaiseminen

In[1]:=

•Ensimmäisen ja toisen asteen yhtälöt; yleisemmin: polynomiyhtälöt

Luontevinta on aloittaa tallettamalla yhtälö jollekin (kuvaavalle) nimelle. Yhtälön yhtäläisyysmerkki on kaksi peräkkäistä yhtäläisyysmerkkiä; yksi yhtäläisyysmerkki on sijoitusoperaattori, jolla lauseke talletetaan jollekin nimelle.

In[2]:=

Out[2]=

Ratkaisu saadaan komennolla Solve, jolle on annettava kaksi argumenttia: yhtälö ja tuntematon, so. symboli, jonka suhteen yhtälö halutaan ratkaista:

In[3]:=

Out[3]=

Yhtä hyvin yhtälö voidan suoraan kirjoittaa Solve-komennon argumentiksi:

In[4]:=

Out[4]=

Ratkaisu saadaan korvaussäännön muodossa. Muuttujalle x ei aseteta arvoa:

In[5]:=

Out[5]=

Mihin tahansa lausekkeeseen voidaan muuttujalle x sijoittaa saatu arvo korvausoperaattorin /. (eli ReplaceAll) avulla:

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Vastaavasti toisen asteen yhtälölle:

In[8]:=

Out[8]=

In[9]:=

Out[9]=

${{x -> (-b - (b^2 - 4 a c)^(1/2))/(2 a)}, {x -> (-b + (b^2 - 4 a c)^(1/2))/(2 a)}}$

Tämän avulla voidaan laskea esimerkiksi juurten summa ja tulo:

In[10]:=

Out[10]=

In[11]:=

Out[11]=

Korvaussännön ratkaisu eri osiin on tässä viitattu ensin funktioilla First ja Last ja sitten indeksillä.

Vastaavaan tapaan voidaan käsitellä korkeampien asteiden yhtälöitä:

In[12]:=

Out[12]=

${{x -> 2}, {x -> 2 - 13^(1/2)}, {x -> 2 + 13^(1/2)}}$

Joskus tulos voi olla pitkähkö. Seuraavassa muodostetaan yleinen neljännen asteen yhtälön ratkaisukaava, joka talletetaan korvaussäännön muodossa nimelle rtk. Tämä sisältää itse asiassa neljä korvaussääntöä, koska neljännen asteen yhtälöllä on neljä juurta.

In[13]:=

Out[13]=

In[14]:=

Out[14]=

${{x -> -b/(4 a) - 1/2 √ (b^2/(4 a^2) - (2 c)/(3 a) + (2^(1/3) (c^2 - 3 b d + 12 a e)) ... c^2 - 3 b d + 12 a e)^3 + (2 c^3 - 9 b c d + 27 a d^2 + 27 b^2 e - 72 a c e)^2)^(1/2))^(1/3)))))}}$

Saadun ratkaisukaavan pätevyyttä voidaan testata muodostamalla ensin polynomi, jonka nollakohdat tiedetään, ja yrittämällä sitten ratkaista nämä edellä saadusta yleisestä kaavasta. Polynomi olkoon

In[15]:=

Out[15]=

Sijoitetaan kertoimet edellä saatuun kaavaan ja yritetään sieventää:

In[16]:=

Out[16]=

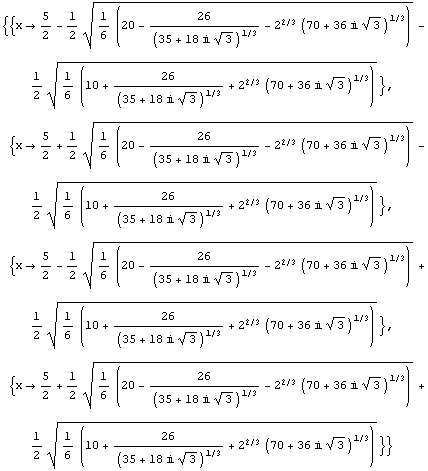
${{x -> 5/2 - 1/2 (1/6 (20 - 26/(35 + 18 i 3^(1/2))^(1/3) - 2^(2/3) (70 + 36 i 3^(1/2))^(1/3 ... ^(1/2) + 1/2 (1/6 (10 + 26/(35 + 18 i 3^(1/2))^(1/3) + 2^(2/3) (70 + 36 i 3^(1/2))^(1/3)))^(1/2)}}$

In[17]:=

Out[17]=

Aina ei kuitenkaan onnistu. Muodostetaan uusi neljännen asteen polynomi ja ratkaistaan se toisaalta suoraan Solve-komennolla, toisaalta sijoittamalla polynomin kertoimet ratkaisukaavaan.

In[18]:=

Out[18]=

In[19]:=

Out[19]=

Nämä ovat todellakin nollakohdat:

In[20]:=

Out[20]=

Mutta:

In[21]:=

$General :: stop : Further output of Power :: \" infy \" will be suppressed during this calculation.$

Out[21]=

Saatu ratkaisukaava ei siis olekaan aivan yleinen!

•Polynomiyhtälöt numeerisesti

Polynomiyhtälön ratkaiseminen ei aina ole suoraviivaista:

In[22]:=

Out[22]=

In[23]:=

Out[23]=

${{x -> Root[1 + #1 + #1^7 &, 1]}, {x -> Root[1 + #1 + #1^7 &, 2]}, {x -> Root ... + #1^7 &, 5]}, {x -> Root[1 + #1 + #1^7 &, 6]}, {x -> Root[1 + #1 + #1^7 &, 7]}}$

Nämä ovat kyllä polynomin nollakohdat, mutta niiden lausekkeet ovat hieman erikoiset. Taustalla on vakava periaatteellinen rajoitus: juurilausekkeiden (neliöjuuri, kuutiojuuri jne.) avulla ilmaistavat yleiset ratkaisukaavat ovat olemassa ainoastaan neljänteen asteeseen saakka. Korkeampien asteiden polynomeille voidaan käyttää eo. lausekkeiden tapaisia ilmauksia, jotka ovat oikeastaan vain tautologioita. Numeeriset arvot saadaan kuitenkin tällöinkin:

In[24]:=

Out[24]=

Toisaalta numeeriset arvot voidaan laskea myös suoraan funktiolla NSolve, mikä saattaa olla oleellisestikin nopeampaa:

In[25]:=

Out[25]=

•Transkendenttiyhtälöt

Joissakin tapauksissa funktiota Solve voidaan käyttää myös muiden kuin polynomiyhtälöiden ratkaisuun:

In[26]:=

Out[26]=

${{x -> -(3 π)/4}, {x -> π/4}, {x -> -ArcCos[-(1/2 - 1/2 (1/2 - 1/(2 2^(1/2) ... + 1/(2 2^(1/2)))^(1/2))^(1/2)]}, {x -> ArcCos[(1/2 + 1/2 (1/2 + 1/(2 2^(1/2)))^(1/2))^(1/2)]}}$

In[27]:=

Out[27]=

Kaikkia juuria ei kuitenkaan saada.

Yleensä ns. transkendenttiyhtälöiden ratkaiseminen ei kuitenkaan onnistu:

In[28]:=

Out[28]=

Tällaisten yhtälöiden numeeriseen ratkaisemiseen on käytettävissä funktio FindRoot. Se käyttää Newtonin menetelmän tyyppistä (mutta tehokkaampaa) algoritmia yhtälön yhden ratkaisun löytämiseen. Algoritmille on annettava jonkinlainen etsittävän juuren alkuapproksimaatio:

In[29]:=

Out[29]=

In[30]:=

Out[30]=

In[31]:=

Out[31]=

Menetelmä ei aina anna alkuapproksimaatiota lähintä juurta, kuten viimeinen esimerkeistä osoittaa.

Alkuarvojen etsimisessä voidaan käyttää graafisia esityksiä:

In[32]:=

[Graphics:HTMLFiles/luento2_69.gif]

Out[32]=

•Yhtälöryhmät

Kaikkia edellä esitettyjä menetelmiä voidaan käyttää myös yhtälöryhmien ratkaisemiseen. Funktioissa Solve ja NSolve niin yhtälöt kuin tuntemattomatkin on tällöin annettava aaltosulkuihin suljettuina listoina:

In[33]:=

Out[33]=

In[34]:=

$Solve[{u^2 + v^2 == 1, v == u^2}, {u, v}]$

Out[34]=

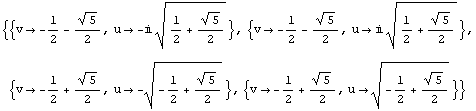
${{v -> -1/2 - 5^(1/2)/2, u -> -i (1/2 + 5^(1/2)/2)^(1/2)}, {v -> -1/2 - 5^(1/2)/2, u ... u -> -(-1/2 + 5^(1/2)/2)^(1/2)}, {v -> -1/2 + 5^(1/2)/2, u -> (-1/2 + 5^(1/2)/2)^(1/2)}}$

In[35]:=

$NSolve[{u^2 + v^2 == 1, v == u^2}, {u, v}]$

Out[35]=

Funktion FindRoot syntaksi on hieman erilainen:

In[36]:=

$FindRoot[{u^2 + v^2 == 1, v == u^2}, {u, 1}, {v, 1}]$

Out[36]=

Converted by Mathematica (May 8, 2003)