Simo K. Kivelä / 28.04.2003

Mathematica numeerisena ja symbolisena laskimena

•Mitä laskentaohjelmalta voi odottaa?

Periaatteessa interaktiivinen symbolinen laskentaohjelma on kuin laajennettu taskulaskin: voidaan laskea numeerisia arvoja lausekkeille, muokata (sieventää eri tavoin, derivoida, integroida jne.) symbolisia, ts. kirjaimia sisältäviä lausekkeita, laatia erilaisia graafisia esityksiä (funktioiden kuvaajia, tilastoja yms.), kirjoittaa ohjelmakoodeja ohjelman omalla kielellä, tallettaa syötteet ja tulosteet dokumentiksi, joka voidaan varustaa selittävillä teksteillä, jne. Dokumentti voidaan tulostaa paperille tai muuntaa www-sivuiksi. Tämä esitys on juuri tällainen dokumentti.

Laskentaohjelmat on perinteisesti jaettu numeerisiin ja symbolisiin. Edelliset laskevat ainoastaan numeerisia laskuja, jälkimmäiset kykenevät käsittelemään myös lausekkeita. Molemmissa on yleensä mahdollisuudet graafisten esitysten tekemiseen. Nykyään ero on hämärtynyt: symboliset ohjelmat ovat yleensä erittäin tehokkaita myös numeerisessa laskennassa, alunperin numeerisiin ohjelmiin on liitetty symbolisen laskennan mahdollistavia komponentteja.

Tunnetuimmat ja laajimpaan käyttöön levinneet symboliset ohjelmat ovat Mathematica ja Maple. Kolmantena kannattanee mainita muPad. Myös ilmaisia ohjelmia on saatavissa (esimerkiksi Maxima, Yacas), mutta ominaisuuksiltaan nämä ovat vaatimattomampia ja usein hieman vanhahtavia. Numeerisista ohjelmista merkittävimmät ovat Matlab ja Mathcad. Kummassakin on nykyään myös symbolisia ominaisuuksia, jotka ovat peräisin mukaan liitetyistä Maple-ohjelman komponenteista.

Tämä on Mathematica-dokumentti (notebook = muistikirja) ja esittelee Mathematica-ohjelman perusominaisuudet.

•Yleistä

Ohjelma tallettaa muistiin kaikki syötteet ja välitulokset. Näihin voidaan missä tahansa laskennan vaiheessa viitata tulostuksen numerolla
(esimerkiksi Out[12] tai %12). Jos tulokselle on annettu nimi (mikä on suositeltavaa), siihen voidaan viitata myös tällä nimellä.

Pitkässä istunnossa saattaa aiheutua ongelmia siitä, että muistissa on vanhoja tuloksia talletettuna nimellä, jonka käyttäjä jo on unohtanut tai jonka hän kuvittelee tarkoittavan jotakin muuta. Tämän johdosta kannattaa uuteen tehtävään ryhdyttäessä muisti puhdistaa hieman kryptisellä komennolla:

In[1]:=

•Numeerinen laskenta

Numeerisessa laskennassa voidaan käyttää periaatteessa mielivaltaisen monta numeroa. Käytännössä koneen muisti ja laskenta-aika asettavat rajoituksensa. Käytetty syntaksi on luonnollinen. Kertomerkki on joko välilyönti tai *; pois sitä ei voida (yleensä) jättää. Kuten seuraavat esimerkit osoittavat, pelkän välilyönnin käyttäminen ei ole kovin selkeätä ainakaan numeerisissa laskuissa.

In[2]:=

Out[2]=

In[3]:=

Out[3]=

Kertoma ilmaistaan tavalliseen tapaan huutomerkillä.

In[4]:=

Out[4]=

Luku π syötetään nimellä Pi tai se voidaan valita valikosta. Funktiolla N sille voidaan laskea haluttu määrä desimaaleja. (Desimaaleja tunnetaan nykyään hieman yli 206 miljardia. Kovin monen desimaalin laskeminen tukkii Mathematican varsin tehokkaasti.)

In[5]:=

Out[5]=

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Laskettuihin arvoihin voidaan myöhemmin viitata:

In[8]:=

Out[8]=

In[9]:=

Out[9]=

In[10]:=

Out[10]=

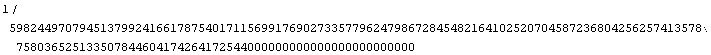
1/598244970794513799241661787540171156991769027335779624798672845482164102520704587236804256257413578758036525133507844604174264172544000000000000000000000000

Viittaamisesta tulee helpompaa, jos tuloksille annetaan nimet (mielellään mahdollisimman kuvaavat nimet, jolloin on itsekin helpompi muistaa, mitä mikin symboli tarkoittaa):

In[11]:=

Out[11]=

In[12]:=

Out[12]=

In[13]:=

Out[13]=

Jos syötteessä on desimaaliluku (jossa käytetään desimaalipistettä, ei -pilkkua), tulos lasketaan desimaalilukuna, muutoin lasketaan ns. tarkoilla arvoilla.

In[14]:=

Out[14]=

In[15]:=

Out[15]=

Myös funktioiden arvoja voidaan laskea:

In[16]:=

Out[16]=

In[17]:=

Out[17]=

In[18]:=

Out[18]=

In[19]:=

Out[19]=

Myös kompleksiluvuilla voidaan laskea:

In[20]:=

Out[20]=

In[21]:=

Out[21]=

In[22]:=

Out[22]=

In[23]:=

Out[23]=

•Symbolinen laskenta

Vastaavalla tavalla voidaan käsitellä algebrallisia lausekkeita, so. lausekkeita, joissa on kirjainsymboleja:

In[24]:=

Out[24]=

Lausekkeita voidaan muokata, esimerkiksi sieventää useilla eri tavoilla. Ei ole itsestään selvää, mitä sievä kussakin tapauksessa tarkoittaa; se riippuu siitä, mitä lausekkeelle on seuraavaksi tarkoitus tehdä. Tämän johdosta sieventämiskomentoja on useita erilaisia eikä niiden hallinta aina ole helppoa. Kunkin komennon argumentti (lauske, johon operaatio kohdistuu) annetaan hakasuluissa. Tämä on yleinen tapa merkitä funktioita Mathematicassa; funktiotahan nämä komennotkin ovat. Esimerkkeinä lausekkeen kehittäminen, tekijöihin jako ja ns. osamurtokehitelmän muodostaminen; erilaisia sievennyskomentoja on kuitenkin paljon enemmän.

In[25]:=

Out[25]=

In[26]:=

Out[26]=

In[27]:=

Out[27]=

In[28]:=

Out[28]=

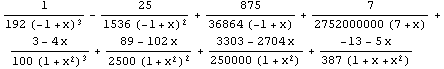
1/(192 (-1 + x)^3) - 25/(1536 (-1 + x)^2) + 875/(36864 (-1 + x)) + 7/(2752000000 (7 + x)) + (3 ... - 102 x)/(2500 (1 + x^2)^2) + (3303 - 2704 x)/(250000 (1 + x^2)) + (-13 - 5 x)/(387 (1 + x + x^2))

Yleisiä sievennyskomentoja ovat Simplify ja FullSimplify. Mitä nämä tekevät, ei kuitenkaan ole aina selvää:

In[29]:=

Out[29]=

In[30]:=

Out[30]=

In[31]:=

Out[31]=

In[32]:=

Out[32]=

In[33]:=

Out[33]=

In[34]:=

Out[34]=

Funktioiden käsittelyyn liittyy omat sievennyskomentonsa:

In[35]:=

Out[35]=

Kaikki yhden argumentin sievennyskomennot voidaan kirjoittaa myös argumentin jälkeen:

In[36]:=

Out[36]=

In[37]:=

Out[37]=

Derivointi ja integrointi tapahtuvat yksinkertaisesti.

In[38]:=

Out[38]=

In[39]:=

Out[39]=

In[40]:=

Out[40]=

In[41]:=

Out[41]=

In[42]:=

$Integrate[x^5 Exp[-x], {x, 0, 1}]$

Out[42]=

Mathematica kuitenkin tuntee tavallisten alkeisfunktioiden lisäksi melkoisen määrän myös ns. erikoisfunktioita.

In[43]:=

$Integrate[Exp[-t^2], {t, 0, 2}]$

Out[43]=

Tälle saadaan myös numeerinen arvo:

In[44]:=

Out[44]=

Integrointi voi tapahtua myös numeerisesti:

In[45]:=

$NIntegrate[Exp[-t^2], {t, 0, 2}]$

Out[45]=

Virheellisiä tuloksia voi kuitenkin yllättäen syntyä. Jos integroidaan symbolisesti ja tuloksesta lasketaan numeerinen arvo, saatetaan saada eri tulos kuin integroimalla suoraan numeerisesti. Vielä Mathematican edellinen versio sai seuraavista syötteistä eri tulokset. Kyseessä on sinänsä ymmärrettävä ongelma, joka aiheutuu kyseisen erikoisfunktion (EllipticE) ominaisuuksista kompleksialueella. Mikään ohjelmisto tuskin on virheetön: uudessa versiossa on uudet virheet. Käyttäjän tulee siis oppia kriittisyyteen.

In[46]:=