Simo K. Kivelä / 06.08.2001

Frégier'n lause ellipsille

•Tehtävä

Ellipsin kehältä valitaan piste . Tämän kautta asetetaan kaksi toisiaan vastaan kohtisuoraa suoraa, jotka leikkaavat ellipsin pisteen lisäksi pisteissä ja . Osoita, että on olemassa suorien asennosta riippumaton piste , jonka kautta jana AB kulkee.

•Ratkaisu

In[1]:=

Muodostetaan origokeskisen ellipsin yhtälö:

In[2]:=

Out[2]=

Jokainen tämän kehäpiste voidaan esittää seuraavassa muodossa:

In[3]:=

Out[3]=

Kaikki ellipsin pisteet saadaan, kun parametrille annetaan arvot väliltä . Pisteet todellakin toteuttavat ellipsin yhtälön:

In[4]:=

Out[4]=

Tämän pisteen kautta asetetaan kaksi toisiaan vastaan kohtisuoraa suoraa. Annetaan nämä vektorimuodossa, jolloin suuntavektorit voidaan kirjoittaa ja . Vektoriesityksessä tarvittava parametri olkoon :

In[5]:=

Out[5]=

In[6]:=

Out[6]=

Etsitään kummankin suoran ja ellipsin leikkauspisteet. Näitä on kummallakin suoralla kaksi ja niistä toinen on luonnollisesti ellipsillä oleva piste ${x _ 0, y _ 0}$ , jonka kautta suorat asetettiin. Sievennetään ratkaisujen lausekkeet.

In[7]:=

Out[7]=

${{u -> -(2 a b (b p Cos[t] + a q Sin[t]))/(b^2 p^2 + a^2 q^2), x -> (a ((-b^2 p^2 + a^2 ... - a q) (b p + a q) Sin[t]))/(b^2 p^2 + a^2 q^2)}, {u -> 0, x -> a Cos[t], y -> b Sin[t]}}$

In[8]:=

Out[8]=

${{u -> 0, x -> a Cos[t], y -> b Sin[t]}, {u -> (2 a b (b q Cos[t] - a p Sin[t]))/( ... p^2 + b^2 q^2), y -> (b (2 a b p q Cos[t] + (-a^2 p^2 + b^2 q^2) Sin[t]))/(a^2 p^2 + b^2 q^2)}}$

Edellisessä tapauksessa jälkimmäinen ratkaisu antaa suorien yhteisen pisteen. Jälkimmäisessä tapauksessa tämä on edellinen. Talletetaan saatujen toisten leikkauspisteiden koordinaatit omille nimilleen:

In[9]:=

Out[9]=

${(a ((-b^2 p^2 + a^2 q^2) Cos[t] - 2 a b p q Sin[t]))/(b^2 p^2 + a^2 q^2), (b (-2 a b p q Cos[t] + (b p - a q) (b p + a q) Sin[t]))/(b^2 p^2 + a^2 q^2)}$

In[10]:=

Out[10]=

${(a ((a p - b q) (a p + b q) Cos[t] + 2 a b p q Sin[t]))/(a^2 p^2 + b^2 q^2), (b (2 a b p q Cos[t] + (-a^2 p^2 + b^2 q^2) Sin[t]))/(a^2 p^2 + b^2 q^2)}$

Saadut kaksi pistettä määräävät suoran. Tällöin ellipsin sisään syntyy suorakulmainen kolmio, jonka hypotenuusana on viimeksi muodostettu suora. Hypotenuusasuoran tavanomainen yhtälö:

In[11]:=

Out[11]=

y - (b (-2 a b p q Cos[t] + (b p - a q) (b p + a q) Sin[t]))/(b^2 p^2 + a^2 q^2) == ((x - (a ( ... (b^2 p^2 + a^2 q^2) + (a ((a p - b q) (a p + b q) Cos[t] + 2 a b p q Sin[t]))/(a^2 p^2 + b^2 q^2))

Jotta tilanteesta voidaan piirtää kuvio, ilmoitetaan Mathematicalle, että tarvitaan lisäpaketti:

In[12]:=

Muodostetaan kohtisuorien suorien tavanomaiset yhtälöt eliminoimalla vektoriesityksestä parametri:

In[13]:=

Out[13]=

In[14]:=

Out[14]=

Kuvio piirretään seuraavilla lukuarvoilla:

In[15]:=

Out[15]=

In[16]:=

[Graphics:HTMLFiles/fregier_41.gif]

Out[16]=

Kuvaan voidaan myös lisätä tekstit ja merkitä piste :

In[17]:=

Out[17]=

In[18]:=

[Graphics:HTMLFiles/fregier_47.gif]

Out[18]=

Frégier'n lause väittää, että suora AB kulkee aina saman pisteen kautta riippumatta kohtisuorien suorien asennosta; ellipsin piste , jonka kautta kohtisuorat asetetaan, pidetään kuitenkin kiinteänä.

Lause voidaan todistaa asettamalla kohtisuorat toiseen asentoon ja määrittämällä tätä tilannetta vastaava jana AB. Jos saatujen kahden AB-janan leikkauspiste ei riipu suuntavektorista , lause on todistettu.

Muodostetaan toinen AB-suora mahdollisimman yksinkertaisesti:

In[19]:=

Out[19]=

y - (b (-2 a b r s Cos[t] + (b r - a s) (b r + a s) Sin[t]))/(b^2 r^2 + a^2 s^2) == ((x - (a ( ... (b^2 r^2 + a^2 s^2) + (a ((a r - b s) (a r + b s) Cos[t] + 2 a b r s Sin[t]))/(a^2 r^2 + b^2 s^2))

Ratkaistaan AB-suorien leikkauspiste ja sievennetään se:

In[20]:=

In[21]:=

Out[21]=

${(a (a^2 - b^2) Cos[t])/(a^2 + b^2), (b (-a^2 + b^2) Sin[t])/(a^2 + b^2)}$

Tulos on todellakin riippumaton symboleista , , ja , ts. kohtisuorien suoraparien suunnista.

Ratkaisu ei luonnollisestikaan mene edellä esitetyllä tavalla, jos ja . Tätä ei laskussa ole mitenkään suljettu pois. Mathematica kuitenkin käsittelee tällaisessa tilanteessa ns. geneeristä tapausta, ts. tapausta, missä mitään rajoittavia erikoisehtoja ei vallitse.

Frégier'n lause on siis saatu todistetuksi.

Esimerkkitapauksessa hypotenuusasuorien leikkauspiste on

In[22]:=

Out[22]=

Kuvio:

In[23]:=

Out[23]=

In[24]:=

[Graphics:HTMLFiles/fregier_67.gif]

Out[24]=

In[25]:=

[Graphics:HTMLFiles/fregier_70.gif]

Out[25]=

Animaatio:

In[26]:=

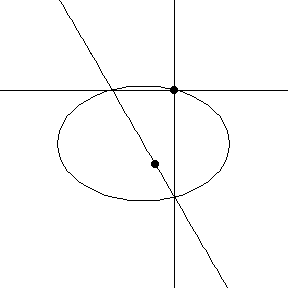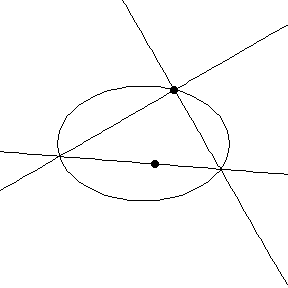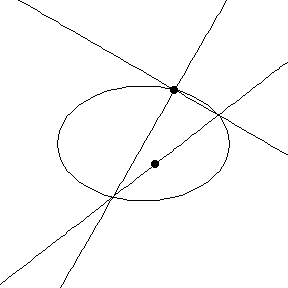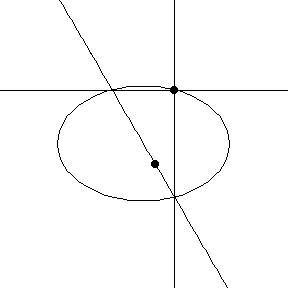
animaatio

•Lisäongelma

Lisäongelmana voidaan pohtia seuraavaa: Edellä esitetyn mukaisesti jokaista ellipsin kehän pistettä kohden saadaan AB-suorien leikkauspiste. Jos kehäpiste kiertää koko ellipsin, millaisen käyrän piirtää hypotenuusasuorien leikkauspiste?

Leikkauspiste on edellä lasketun mukaisesti

In[27]:=

Out[27]=

${(a (a^2 - b^2) Cos[t])/(a^2 + b^2), (b (-a^2 + b^2) Sin[t])/(a^2 + b^2)}$

Tämä on itse asiassa etsityn käyrän parametriesitys parametrina . Käyrän yhtälö saadaan eliminoimalla parametri yhtälöistä

In[28]:=

Out[28]=

${x == (a (a^2 - b^2) Cos[t])/(a^2 + b^2), y == (b (-a^2 + b^2) Sin[t])/(a^2 + b^2)}$

Eliminointi tapahtuu esimerkiksi seuraavasti:

In[29]:=

$yhtalot = Flatten[{paramyhtalot /. {Sin[t] -> s, Cos[t] -> c}, s^2 + c^2 == 1}]$

Out[29]=

${x == (a (a^2 - b^2) c)/(a^2 + b^2), y == (b (-a^2 + b^2) s)/(a^2 + b^2), c^2 + s^2 == 1}$

In[30]:=

Out[30]=

Lopuksi kuvio, jossa on sekä alkuperäinen ellipsi että etsitty uusi käyrä, joka myös on ellipsi:

In[31]:=

[Graphics:HTMLFiles/fregier_84.gif]

Out[31]=

Converted by Mathematica (May 15, 2003)