Mat-1.433/443 K3/P3 välikoe 1
17.10.2005 HA
Alustukset
| > |
with(inttrans): alias(L=laplace,IL=invlaplace,u=Heaviside):
|
Teht. 1
(a)
| > |
argument(-1+I*sqrt(3));
|
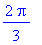
Kyseessähän on kolmio, jonka kateetit ovat 1 ja
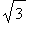 ja hypotenuusa 2, kulmat ovat
ja hypotenuusa 2, kulmat ovat
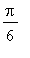 ja
ja
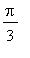 . (Vrt. harj. tehtävän mallivastaus).
. (Vrt. harj. tehtävän mallivastaus).
Koska
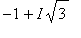 on toisessa koordinaattineljänneksessä, on argumentti tosiaankin
on toisessa koordinaattineljänneksessä, on argumentti tosiaankin
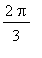 (eli 120 astetta). Siis:
(eli 120 astetta). Siis:
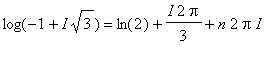 .
.
Annetaan vielä Maplenkin laskea:
| > |
log(-1+I*sqrt(3)); evalc(%):simplify(%,symbolic);
|
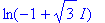
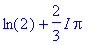
(b)
Warning, the name changecoords has been redefined
| > |
conformal(z,z=log(0.5)-Pi*I/2..Pi*I,grid=[20,20],numxy=[20,20]);conformal(exp(z),z=log(0.5)-Pi*I/2..Pi*I,grid=[20,20],numxy=[50,50],scaling=constrained);
|
![[Maple Plot]](images/vk110.gif)
![[Maple Plot]](images/vk111.gif)
Teht. 2
(a)
| > |
f:=convert(sinh(z),exp);subs(z=x+I*y,%);
|
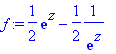
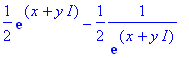
| > |
expand(%);evalc(%):subs(cos(y)^2+sin(y)^2=1,%);
|
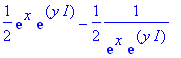
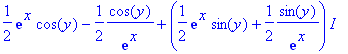
Tästä muodosta näkyy suoraan:
- Re-osa: Otetaan cos(y) tekijäksi, toiseksi tulee sinh(x).
- Im-osa: Otetaan sin(y) tekijäksi, toiseksi tulee cosh(x).
| > |
f:=sinh(x)*cos(y)+I*cosh(x)*sin(y);
|
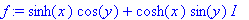
| > |
evalc(sinh(x+I*y)); # Tarkistus käy näin helposti.
|
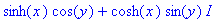
(b)
| > |
u:=sinh(x)*cos(y); v:=cosh(x)*sin(y);
|
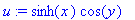
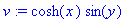
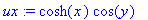
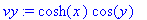
Siis 1. CR-yhtälö
![u[x] = v[y]](images/vk122.gif) pätee. Entä toinen:
pätee. Entä toinen:
| > |
uy:=diff(u,y); vx:=diff(v,x);
|
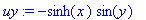
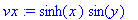
Pätee sekin, nimittäin
![u[y] = -v[x]](images/vk125.gif) .
.
Koska osittaisderivaatat ovat jatkuvia ja Cauchy-Riemannin yhtälöt ovat voimassa koko kompleksitasossa, on funktio sinh(z)
analyyttinen koko kompleksitasossa (eli "kokonainen", "entire").
Teht. 3
| > |
restart:with(inttrans): alias(L=laplace,IL=invlaplace,u=Heaviside):
|
| > |
f1:= piecewise(t < 1,t,t>1 and t < 2,1,0);
|
![f1 := PIECEWISE([t, t < 1],[1, -t < -1 and t < 2],[0, otherwise])](images/vk126.gif)
![[Maple Plot]](images/vk127.gif)
Ratkaisu 1) Suoraan määritelmän mukaan
| > |
Int(t*exp(-s*t),t=0..1)+Int(exp(-s*t),t=1..2):% = value(%);
|
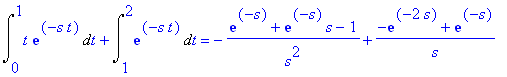
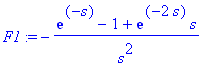
Ratkaisu 2) Kirjoitetaan u-funktion avulla:
| > |
f1:=t*(u(t)-u(t-1))+(u(t-1)-u(t-2));
|
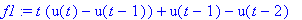
| > |
# t*u(t-1) kirjoitetaan:
|
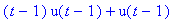
| > |
f1:=t*u(t)-((t-1)*u(t-1)+u(t-1))+(u(t-1)-u(t-2));
|
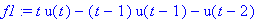
Katsotaan termeittäin:
| > |
L(t*u(t),t,s); # Tämähän on sama kuin funktion f(t)=t muunnos.
|
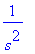
| > |
L((t-1)*u(t-1),t,s); # t:n muunnos = 1/s^2, t-siirrosta aiheutuu kertoja exp(-s)
|
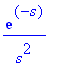
| > |
L(u(t-2),t,s); # Tässä on suoraan u(t-2):n muunnos:
|
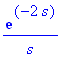
Yhdistämällä saadaan:
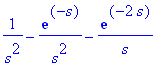
| > |
F[2](s):=(2*s+7)/(s^2+2*s+5);
|
 := (2*s+7)/(s^2+2*s+5)](images/vk137.gif)
Täydennetään nimittäjässä neliöksi:
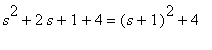 .
.
Osoittajaan pitää saada myös
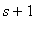 , jotta voidaan soveltaa s-siirtoa. Kirjoitetaan siis osoittaja muotoon
, jotta voidaan soveltaa s-siirtoa. Kirjoitetaan siis osoittaja muotoon
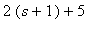
Nyt
 = G(s+1)](images/vk141.gif) , missä
, missä
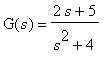 .
.
Nyt saadaan s-siirtolausella käänteismuunnoskaava:
 = exp(-t)*g(t)](images/vk143.gif) , missä
, missä
![f[2]](images/vk144.gif) ja
ja
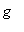 tarkoittavat käänteismuunnoksia tavalliseen tapaan.
tarkoittavat käänteismuunnoksia tavalliseen tapaan.
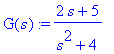
| > |
g(t):=IL(G(s),s,t); # Käänteismuunnos
|
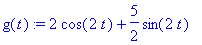
 = exp(-t)*(2*cos(2*t)+5/2*sin(2*t))](images/vk148.gif)
Tarkistukseksi annetaan Maplen laskea suoraan:
| > |
'IL'(F[2](s),s,t) = IL(F[2](s),s,t);
|
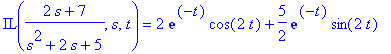
Oikein meni !
Teht. 4
| > |
with(inttrans): alias(L=laplace,IL=invlaplace,u=Heaviside):
|
| > |
diffyht:=diff(y(t),t,t)+2*y(t)=u(t)-u(t-1);
|
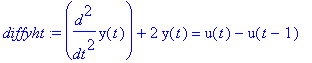
| > |
plot(u(t)-u(t-1),t=0..2,scaling=constrained,axes=frame);
|
![[Maple Plot]](images/vk151.gif)
| > |
Ldy:=L(diffyht,t,s); # Laplace-muunnetaan
|
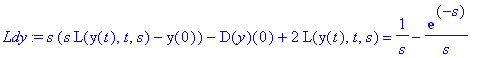
| > |
Ldy:=subs(y(0)=0,D(y)(0)=0,Ldy); # Alkuehdot (0)
|
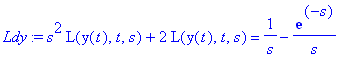
| > |
Y:=solve(Ldy,L(y(t),t,s)); # Ratkaistaan L-muunnos Y:
|
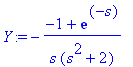
Kirjoitetaan muotoon
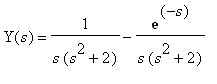
Y(s) = 1/(s*(s^2+2)) - exp(-s)/(s*(s^2 + 2))
| > |
Y1(s):=1/(s^2 + 2);Y2(s):=1/(s*(s^2+2));
|
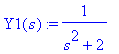
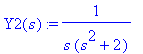
Jälkimmäiseen voidaan käyttää joko integraalin muunnosta (konvoluutiolauseen erikoistapaus) tai osamurtoa.
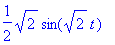
| > |
y1:=t->1/2*2^(1/2)*sin(2^(1/2)*t);
|
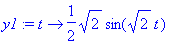
Integraalin muunnos menee helposti, tarvitsee vain integroida sini.
| > |
y2(t)= Int(y1(tau),tau=0..t); y2:=unapply(int(y1(tau),tau=0..t),t);
|
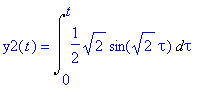
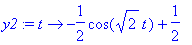
Vaihtoehtoisesti osamurtona
. Tätä on ohjeen mukaan haettava muodossa
| > |
Y2(s) = A/s + (B*s+C)/(s^2+2);
|
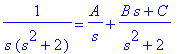
Jos kerrotaan s:llä ja sijoitetan s=0, saadaan heti A= 1/2 . Muita kertoimia varten lienee parasta vain kiltisti kertoa samalle viivalle.
| > |
A/s+(B*s+C)/(s^2+2); simplify(%): Y2(s)=collect(%,{s,s^2});
|
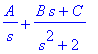
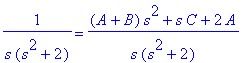
Saadaan heti: C=0, A=1/2 , B = - 1/2 (A saatiin tästäkin aivan suoraan.) Siispä
| > |
Y2(s):=convert(Y2(s),parfrac,s);
|
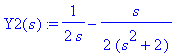
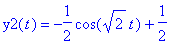
Saatiinpa sama näinkin! Muistetaan tilanne:
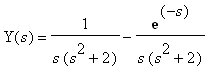
Siispä:
| > |
y(t) = y2(t)-y2(t-1)*u(t-1);
|
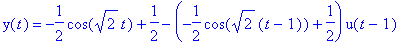
Annetaan Maplen käänteismuuntaa suoraan:
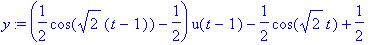
Samat ovat, joten tämäkin lasku meni putkeen!
| > |
plot([u(t)-u(t-1),y],t=0..7,color=[red,blue],title="Punainen heräte, sininen vaste");
|
![[Maple Plot]](images/vk170.gif)
Kun vaimennusta ei ole, värähtely jatkuu ikuisesti samalla amplitudilla.
![]()
![]() ja hypotenuusa 2, kulmat ovat
ja hypotenuusa 2, kulmat ovat
![]() ja
ja
![]() . (Vrt. harj. tehtävän mallivastaus).
. (Vrt. harj. tehtävän mallivastaus).
![]() on toisessa koordinaattineljänneksessä, on argumentti tosiaankin
on toisessa koordinaattineljänneksessä, on argumentti tosiaankin
![]() (eli 120 astetta). Siis:
(eli 120 astetta). Siis:
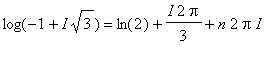 .
.
![]()
![]()
![[Maple Plot]](images/vk110.gif)
![[Maple Plot]](images/vk111.gif)
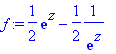
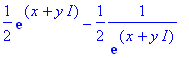
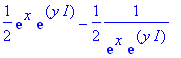
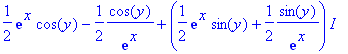
![f1 := PIECEWISE([t, t < 1],[1, -t < -1 and t < 2],[0, otherwise])](images/vk126.gif)
![[Maple Plot]](images/vk127.gif)
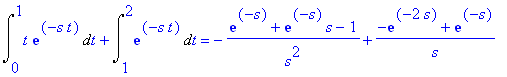
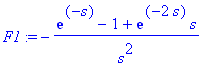
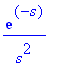
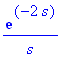
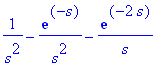
 := (2*s+7)/(s^2+2*s+5)](images/vk137.gif)
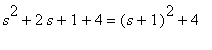 .
.
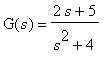 .
.
 = exp(-t)*g(t)](images/vk143.gif) , missä
, missä
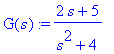
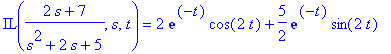
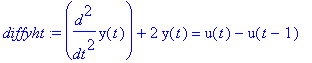
![[Maple Plot]](images/vk151.gif)
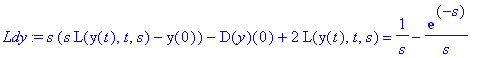
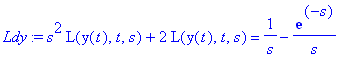
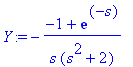
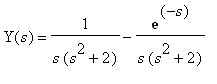
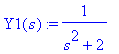
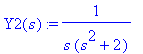
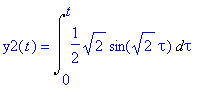
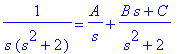
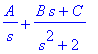
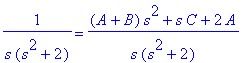
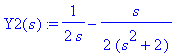
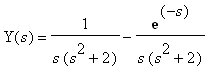
![[Maple Plot]](images/vk170.gif)