
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
MATLAB-tehtäviä koskien epälineaaristen yhtälöiden numeerista ratkaisemista.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. Historiallisesti mielenkiintoinen yhtälö on
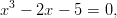
jota Wallis-niminen matemaatikko käsitteli, kun hän ensi kertaa esitteli Newtonin menetelmää Ranskan akatemialle. [Lähde: Moler NCM]
- 1.
- Piirrä kuvaaja saadaksesi alkuarvon Newtonin menetelmälle reaalijuurta varten.
- 2.
- Määritä reaalijuuri omanewton:lla Neuvo: Polynomifunktion voit määritellä
tähän tapaan, kun p on kerroinvektori:
pf=@(x) polyval(p,x)
Derivaatan saat polyder- (tai omapolyder)-funktiolla.
- 3.
- Yritä löytää kompleksijuuri antamalla kompleksisia alkuarvoja. (Jos löydät yhden, niin toinen on sen liittoluku.)
- 4.
- Määritä juuret roots-funktion avulla.
Vihje:
Ratkaisu:MlNl01ratk.m[Tulee]
- 2. Määritä funktion
![------x--------
f (x) = 12(x − 1)sin x2 + 0.4x + 0.1 x ∈ [− 4,4 ]](matlabHarNonLin1x.png)
kaikki nollakohdat (33 kpl).
- 3. [NCM 4.15, p. 138]
Keplerin malli:
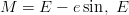
- 1.
- Ratkaise fzero:lla
- 2.
- Sarjakehitelmä:
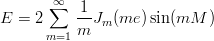
Vihje:
Ratkaisu:MlNl02ratk.m[Tulee]
- 4. [NCM 4.15, p. 138]
Vesiputken syvyys, jotta ei jäädy.
Vihje:
Ratkaisu:MlNlxxratk.m[Tulee]
- 5. Välinpuolitusmenetelmä on eräs tapa löytää funktion nollakohta. Bolzanon lauseen nojalla, jos jatkuvalla funktiolla on jonkin suljetun välin [a,b] päätepisteissä erimerkkiset arvot, sillä on vähintään yksi nollakohta tällä välillä. Välinpuolitusmenetelmä toimii seuraavasti:
- Laske välin [a,b] keskikohta m =
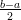 .
.
- Laske f(m). Jos f(m) = 0, ollaan löydetty nollakohta ja lopetetaan algoritmi.
- Jos f(m):n merkki on sama kuin f(a):n, voidaan tutkittavan välin vasenta päätepistetta siirtää kohtaan m, eli a ← m, ja palataan algoritmin kohtaan 1.
- Jos f(m):n merkki on sama kuin f(b):n, voidaan tutkittavan välin oikeaa päätepistetta siirtää kohtaan m, eli b ← m, ja siirrytään algoritmin kohtaan 1.
Tätä ideaa noudattaen, laske funktion f(x) = esin(x2)e−x2 sin(x2) −
 välillä [0, 1]
sijaitseva nollakohta.
Vihje: Numeerisessa tapauksessa absoluuttisen nollan löytäminen on lähes mahdotonta – sinun
tulee määrittää jokin hyväksyttävä toleranssi. Funktion arvojen samanmerkkisyyttä voidaan
tutkia laskemalla näiden tulo: jos kahden luvun tulo on positiivinen, ovat ne samanmerkkisiä.
välillä [0, 1]
sijaitseva nollakohta.
Vihje: Numeerisessa tapauksessa absoluuttisen nollan löytäminen on lähes mahdotonta – sinun
tulee määrittää jokin hyväksyttävä toleranssi. Funktion arvojen samanmerkkisyyttä voidaan
tutkia laskemalla näiden tulo: jos kahden luvun tulo on positiivinen, ovat ne samanmerkkisiä.
- Laske välin [a,b] keskikohta m =
- 6. Sekanttimenetelmä on toinen funktion nollakohtien löytämiseen käytettävä menetelmä. Sekantti on suora joka leikkaa annettua käyrää kahdessa pisteessä. Sekanttimenetelmän idea on approksimoida annettua funktiota f välillä [a,b] pisteiden f(a) ja f(b) välille piirretyllä suoralla. Tämän suoran, ja x-akselin välinen leikkauspiste otetaan välin uudeksi päätepisteeksi. Iteraatiokaavaksi saadaan näin
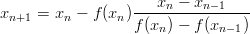
Sekanttimenetelmä suppenee yleensä, mutta ei aina, nopeammin kuin välinpuolitusmenetelmä.
Sekanttimenetelmää käyttäen laske funktion
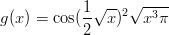
välillä [0, 5] sijaitseva nollakohta. Vihje: Tälle funktiolle ja tälle menetelmälle on mahdollista löytää alkuarvo, jolla menetelmä ei toimi: kokeile siis useaa arvausta.
- 7. Matlab/Maple/Mathematica
H2T17/mlNl100/mplY100/mmaY100Etsi yhtälön x8 −36x7 +546x6 −4536x5 +22449x4 −67284x3 +118124x2 −109584x+40320 = 0 välillä [5.5, 6.5] oleva juuri. Muuta x7:n kerroin luvuksi −36.001 ja katso, mikä vaikutus sillä on juureen.
Vihje: Maple: fsolve
Matlab: roots Mathematica: ...
Ratkaisu: Ratkaisutiedostossa lisää variaatioita ja analyysiä tehtävään.
Avainsanat: Polynomin juuret, numeriikka, häiriöalttius, ill-conditioned - 8. Ratkaise yhtälöryhmä
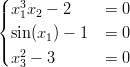
käyttäen Newtonin menetelmää. Tutki suppenemista eri alkuarvoilla. Vihje: Tehtävässä tarvittava Jacobin matriisi kannattaa (ehkä) tehdä spesifinä funktiona.
- 9. Maple,Matlab,[Mathematica] (H2T8)
Newtonin menetelmän askel voidaan määritellä vähäeleisesti Maplelle. Määritellään iterointifunktio:
> N := x -> evalf(x - f(x)/D(f)(x));
Iterointi tapahtuu joko for-silmukalla tai iterointioperaattorilla N@@k. (For silmukka lienee tehokkaampi, kun halutaan muodostaa koko iterointijono.) Ratkaise seuraavat yhtälöt Newtonin menetelmällä. Sopivat alkuarvot vaikkapa kuvan avulla.
- x cos x = sin x + 1, 0 < x < 2π
- x2 + sin x = 8
Vihje: Matlab-tehtävässä on antoisinta tehdä Maple-Matlab-työnjako: Muodostetaan ensin iteraatiokaava Maplella symbolisessa muodossa (jätetään yllä N-kaavasta evalf pois) ja siirretään kaava Matlabiin (lprint, Matlabissa vectorize lisää pisteet.
Kaikkein kätevintä lienee käyttää Symbolic Toolboxia symboliseen derivointiin, jos se on käytettävissä.
Avainsanat: Epälineaarinen yhtälö, Newtonin menetelmä, iteraatio
- 10. Maple , Matlab (H2T9)
Tarkastellaan väestönkasvumallia
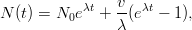
Vihje: Maple: fsolve, Matlab: fzero
Avainsanat: Epälineaarinen yhtälö, väestönkasvumalli, epalineaarinen yhtalo, vaestonkasvumalli.
- 11. Newtonin menetelmä lienee kaikista funktion juuren etsimiseen käytetyistä menetelmistä kuuluisin. Toisin kuin aikaisemmin esittelemämme menetelmät, se ei edellytä tietoa juuren sijainnista, mutta toisaalta se ei aina välttämättä suppene kohti juurta.
Newtonin iteraatioilla tarkasteltavilta funktioilta odotetaan jatkuvuutta ja derivoituvuutta. Newtonin iteraatiokaava on
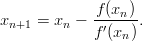
Käyttäen aikaisemmin kirjoittamaasi numeerista derivointikaavaa, ja etsi funktion f(x) = esin(x2)e−x2 sin(x2) −
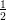 nollakohtia käyttäen Newtonin menetelmää. Käytä
alkuarvoina ainakin arvoja 0.5, 12.2 ja 2.2. Kuten huomataan, alkuarvoilla on todella
dramaattinen vaikutus siihen, kuinka ja minne menetelmä suppenee.
nollakohtia käyttäen Newtonin menetelmää. Käytä
alkuarvoina ainakin arvoja 0.5, 12.2 ja 2.2. Kuten huomataan, alkuarvoilla on todella
dramaattinen vaikutus siihen, kuinka ja minne menetelmä suppenee.
Kokeile sitten ratkaista funktion g(x) = x3 − 2x + 2 nollakohta Newtonin menetelmällä käyttäen alkuarvauksena x0 = 1. Mitä tapahtuu? (vinkki: Ctrl + C lopettaa ikuisen luupin.)
Viimeisenä kokeile ratkaista funktion h(x) = 1 −x2 nollakohta Newtonin menetelmällä käyttäen alkuarvauksena x0 = 0. Mitä tapahtuu? Vihje: Numeerisissa tapauksissa etsitään nollakohtaa jollain sopivalla toleranssilla. Derivaattana kannattaa käyttää määritelmän sijasta 3-pisteen sääntöä:
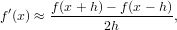
kun h on pieni.
- 12. Kun z = x + iy ja −2 ≤ x,y ≤ 2, eksponenttifunktion z↦ exp(z) kuvaajan voi piirtää seuraavasti:t = -2:0.2:2;
[x y] = meshgrid(t,t);
z = x+i*y;
r = exp(z)
mesh(real(r));Imaginääriosan saa piirrettyä komennolla mesh(imag(r)). Tee vastaavat graafit seuraavista kuvauksista edellämainitulla välillä.
- 1.
- z↦ log(z)
- 2.
- z↦z2
- 3.
- z↦z + 1∕z
- 13. Määritellään
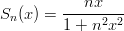
Näytä että jokaiselle kiinnitettylle arvolle x luku Sn(x) lähestyy nollaa, kun n →∞, ja etsi Sn(x):n ääriarvot x:n suhteen. Piirrä funktio Sn(x) välillä [−2, 2] kun n = 2, 4, 6, 8, 10. Vihje: Ohjelman suorituksen voi keskeyttää kesken skriptin komennolla pause. Välin voi määritellä joko vektorinotaatiolla -2:0.02:2 tai komennolla linspace(-2,2,100).
