
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Tehtäviä koskien grafiikan piirtoa MATLABissa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. Piirrä samaan kuvaan funktioiden cos ja sin kuvaajat välillä
![[− 2π, 2π]](matlabHarGrafiikka0x.png) Aloita
tyyliin:
x=linspace(-2*pi,2*pi); y1=cos(x); y2=sin(x);
Aloita
tyyliin:
x=linspace(-2*pi,2*pi); y1=cos(x); y2=sin(x);
plot(...)Vihje: Voit piirtää molemmat yhdellä plot-komennolla tai käyrän kerrallaan pitämällä vanhan kuvan hold-komennon avulla.
Jos haluat kuvat eri grafiikkaikkunoihin, voit käyttää figure-komentoa. Toisinaan on kätevää jakaa grafiikkaruutu osiin. Tämä onnistuu subplot:n avulla. Kokeile näitä vaihtoehtoisia tapoja (nyt tai myöhemmin).
- 2. Piirrä
- 1.
- xe−x2 välillä
![[− 2,2]](matlabHarGrafiikka1x.png)
- 2.
- 1∕(1 + x2) välillä
![[− 4,4 ]](matlabHarGrafiikka2x.png)
Vihje: Muista pisteet laskutoimituksissa!
- 3. Piirrä sin(2x) sinisellä ja cos(5x) punaisella, välillä [−π,π] (samaan kuvaan). Merkitse vielä samaan kuvaan sin(2x):n arvot o-merkeillä x-pisteissä
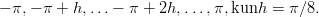
Vihje: Pane merkille tällaiset grafiikan ulkoasua säätelevät lisäkomennot (jotka voidaan antaa jälkikäteen (paitsi hold on pitää antaa ajoissa)):
grid on/off, hold on/off, axis, xlim, ylim, figure, subplot, shg , close all Tutki toiminta help:stä ja oppaista. Aloita: help plot (tai klikkaa: plot). Suorita joitakin kokeiluja (mutta älä uuvuksiin asti tässä vaiheessa vielä). - 4. Piirrä samaan kuvaan funktioiden sin kx kuvaajat välillä
![[0,2π ]](matlabHarGrafiikka4x.png) , kun k = 1…5.
, kun k = 1…5.
- 1.
- Tee nuolinäppäintä ( ↑ ) komentoeditoinnissa hyödyntäen ja hold on- komentoa käyttäen.
- 2.
- Kirjoita pieni for-silmukka.
- 3.
- Muodosta 5-sarakkeinen matriisi, jonka k : s sarake on sin kx, missä x on “x-vektori” .
Vihje: Muodosta ensin 100 × 5-matriisi , jonka sarakkeet ovat kx, k = 1…5. Kätevimmin matriisikertolaskulla x*K, missä x on (100-pituinen) sarakevektori ja K (5-pituinen) indeksi(rivi)vektori. Mieti huolellisesti, miksi!
Toinen mahdollisuus on käyttää meshgrid-komentoa, jonka käyttöön rutinoidutaan 3d-grafiikan yhteydessä. - 5. Matriisiin sovellettuna plot-funktio piirtää kunkin matriisin sarakkeen. Varsin käyttökelpoinen muoto on plot(x,A), jossa x on A:n sarakkeiden pituinen argumenttivektori.
Suorita seuraavat komennot:
>> x=linspace(-1,1);
>> V=vander(x);
>> plot(x,V); shgJatka tähän tapaan:
>> figure % Avaa uusi grafiikkaikkuna.
>> V=fliplr(V);
>> W=V(:,1:10);
>> plot(x,W);shgSelitä, mitä näissä tapahtuu.
- 6. Piirrä samaan kuvaan potenssit x,x2,…,xn, missä n on muuteltava parametri. Käytä m-tiedostoa (skriptiä) seuraavan ohjeen mukaisesti.
Avaa uusi m-tiedosto ( FILE-valikosta open->new->script ) ja talleta se vaikkapa nimelle potenssipiirto.m .
Tai kirjoita komentoikkunassa: >> edit ’potenssipiirto.m’
Aloita tiedosto jotenkin näin:% % Piirret“”a“”an potenssifunktioita.
% Tiedosto: potenssipiirto.m.
% Laatinut Vilja Varis 1.1.2012 % HUOM! ellet muuta tätä, saat 0 pistettä!
close all % Grafiikkaruudun tyhjennys
n=5; % Muuteltava parametri
...Talleta ja kirjoita komentoikkunaan:
>> potenssipiirto
Tällöin tiedostossa olevat Matlab-komennot suorittuvat.
Komennot suorittuvat myös editori-ikkunasta CTR-ENTER :llä. (Mac:ssä yleisesti CTR:n sijasta cmd.)
(Vihreä nuoli tai F5 toimivat myös.)
Suorita skripti muutamalla eri n:n arvollaVihje:
- 1.
- Tee for-silmukka ja käytä hold on-komentoa uuden kuvan piirtämiseksi vanhan kaveriksi.
- 2.
- Olkoon aluksi vaikka n = 3,m = 7, missä m on x-vektorin pituus. Muodosta matriisit
N ja X, missä N koostuu vakiosarakkeista 1,2,3 ja X saadaan latomalla kolme x-saraketta
rinnakkain. Tällöin X.^N on matriisi, jonka sarakkeina ovat x-vektorin potenssit 1,2,3.
Kuva saadaan nyt komennolla plot(x,X.^N). (Yleisesti: plot(x,Y) piirtää kunkin
Y-matriisin sarakkeen x:n toimiessa x-akselina, kun x on Y:n sarakkeiden pituinen vektori.
(Toimii myös riveittäin, jos x on rivien pituinen.)
Miten saadaan helpoimmin matriisit X, N ? Standarditapa on tämä:
>> nind=1:3;
>> [N,X]=meshgrid(nind,x);Suorita ja selvitä itsellesi.
Tee sitten esim. 100-pituinen x-vektori ja vaihtele myös n:ää ja piirrä sileitä kuvia.
Lopuksi voit kokeilla, miltä näyttää mesh(nind,x,X.^N) .Huom! Tällainen meshgrid-komennon käyttö on rutiinitoimenpide 3d-grafiikan tekemisessä, sen toimintaperiaate on mukava ymmärtää, sitä tämä yrittää palvella.
- 3.
- Helpoin tapa lienee Vandermonden matriisi vander. Siitäpä on eri tehtävä (05), mutta ei ole huonoa harjoitella tässäkin uudestaan.
- 7.
[3D-grafiikkaa, korkeuskäyriä] HA
Olkoon
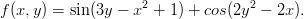
Piirrä pintakuva ja korkeuskäyräpiirros, jälkimmäinen sekä contour että ezcontour-funktioilla. Tässä on mahdollisuus kokeilla korkeuskäyrien valitsemistapoja, myös clabel. Ota alueeksi vaikka [-2 2 -1 1] .
Vihje: Opiskele:
http://math.tkk.fi/˜apiola/matlab/opas/lyhyt/grafiikka.html#sec:3d
Matlab-help: doc mesh, doc surf, doc contour______________________________________Ratkaisu: ./mlG07ratk.m
./html/mlG07ratk.html
http://math.tkk.fi/˜apiola/matlab/opas/lyhyt/ratkaisuja/html/H3teht4.html - 8. Olkoon
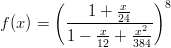
Tämä on exp-funktion rationaaliapproksimaatio, ns. Pade-approksimaatio. Piirrä kuvaaja välillä [0,4].
Piirrä samaan kuvaan exp-funktio eri värillä ja eri kuvaan erotus f(x) −exp(x) Aloita vaikka: x=linspace(0,4,200);Vihje: Tehtävässä harjoitellaan lausekkeen muodostamista pisteittäisin laskutoimituksin.
Homma selkeytyy jakamalla pienempiin osiin, ainakin nyt tällaisiin:>> x=...;
>> osoittaja=...;
>> nimittaja=...;
>> f=...; % Huomaa: f on muuttuja (200-pituinen vektori), ei funktio.
>> % Tässä ei siten saa kirjoittaa: f(x) = ..._________________________________________________________________________________
Ratkaisu:
>> x=linspace(0,4,200);
>> osoittaja=1+x/24; % Skalaarilla jaossa ei tarvia pistettä.
>> % (Jos skalaari jaettaisiin vektorilla, niin toki tarvittaisiin.)
>> nimittaja=1-x/12+x.^2/384;
>> f=(osoittaja./nimittaja).^8;
>> plot(x,f)
>> hold on
>> plot(x,exp(x),’r’)
>> figure % uusi graiikkaikkuna
>> plot(x,f-exp(x))Opettajalle: Tästä voisi tehdä jatkotehtävän tyyppiä: Vertaa Taylorin sarjaa ja Pade-approksimaatiota. Ja vielä: voisi vaikka opettaa, miten Pade-approksimaatioita muodostetaan.
- 9. Olkoot c ja z0 kompleksilukuja. Tällöin rekursion
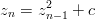
määräämä dynaaminen systeemi tunnetaan kvadraattisena kuvauksena. Valituille luvuille c ja z0 ylläoleva rekursio johtaa kompleksiseen lukujonoon z1,z2,z3…. Tätä jonoa kutsutaan z0:n kiertoradaksi. Riippuen lukujen c ja z0 valinnasta ratojen muotoja on useita.
Annetulle kiinteälle luvulle c useimmilla z0 rata lähestyy ääretöntä (eli |zn| kasvaa rajatta kun n →∞.) Joillakin c ja z0 rata kuitenkin suppenee kohti jotain periodista silmukkaa (eli arvot kiertävät z0 jollain tietyllä etäisyydellä |zn|); joillakin alkuarvoilla rata on kaoottinen. Nämä alkuarvot z0 ovat kuvauksen Julia-joukko.
Tässä harjoituksessa kirjoitetaan MATLAB-ohjelma, joka laskee ns. täytetyn Julia-joukon, joka koostuu niistä alkioista z0 joiden radat jollain annetulla arvolla c eivät kasva rajatta – tavallinen Julia-joukko on tämän joukon reuna.
On näytetty, että jos |zn| kasvaa isommaksi kuin 2 jollain arvolla n, rekursio kasvaa rajatta. Arvoa n jolla tämä tapahtuu, kutsutaan tässä tehtävässä pisteen z0 ”pakonopeudeksi.”
Aloita kirjoittamalla funktio n = escapeVelocity(z0,c,N), jossa N on jokin yläraja pakonopeuksille (erityisesti: jos |zn| < 2∀n < N, funktion tulee palauttaa N. Näin vältetään ikuiset silmukat).
Luodaksesi Julia-joukon kirjoita funktio M=julia(zMax,c,N). Argumentti zMax määrää kompleksitasosta nelikulmion |Im(z)| < zmax,|Re(z)| < zmaz. c ja N ovat samat argumentit kuin edellä, palautettava matriisi M koostuu määritetyn hilan pakonopeuksista.
Aloita funktion julia kirjoittaminen määrittelemällä 500 × 500 hila realitasossa, luo sen avulla vastaava hila Z kompleksitasolle, ja aja funktio escapeVelocity jokaiselle matriisin Z alkiolle. Vihje: Realiakselin väli [a,b] määritellään MATLABissa komennolla I = linspace(a,b,n), missä n on haluttujen pisteiden määrä, kuten esim. 500. Hila reaalitasolle määritellään komennolla [x y] = meshgrid(t1,t2) , missä t1 ja t2 ovat välejä reaaliakselilta. Tästä luodaan kompleksitasoa peittävä hila komennolla z = x+i*y.
Kompleksiluvun modulin saa selville itseisarvofunktiolla abs.
- 10. Piirrä samaan kuvaan funktioiden cos ja sin kuvaajat välillä
![[− 2π, 2π]](matlabHarGrafiikka8x.png) Aloita
tyyliin:
x=linspace(-2*pi,2*pi); y1=cos(x); y2=sin(x);
Aloita
tyyliin:
x=linspace(-2*pi,2*pi); y1=cos(x); y2=sin(x);
plot(...)Vihje: Voit piirtää molemmat yhdellä plot-komennolla tai käyrän kerrallaan pitämällä vanhan kuvan hold-komennon avulla.
Jos haluat kuvat eri grafiikkaikkunoihin, voit käyttää figure-komentoa. Toisinaan on kätevää jakaa grafiikkaruutu osiin. Tämä onnistuu subplot:n avulla. Kokeile näitä vaihtoehtoisia tapoja (nyt tai myöhemmin).
- 11. mlG11.tex
Kirjoita MATLAB-skripti, joka laskee ja piirtää seuraavat funktiot:- a)
- y = 5 cos(3πx). Laske arvo 101:ssä tasavälisessä pisteessä välillä 0 ≤ x ≤
1.
- b)
- y =
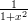 välillä −5 ≤ x ≤ 5 .
välillä −5 ≤ x ≤ 5 .
- c)
- y =
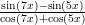 . Laske arvo 200 tasavälisessä pisteessä välillä −
. Laske arvo 200 tasavälisessä pisteessä välillä −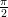 ≤
x ≤
≤
x ≤ 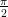 . Käytä axis komentoa asettaaksesi näytettävät akselit väleille
−2 ≤ x ≤ 2 ja −10 ≤ x ≤ 10.
. Käytä axis komentoa asettaaksesi näytettävät akselit väleille
−2 ≤ x ≤ 2 ja −10 ≤ x ≤ 10.
Trigonometriset funktiot toimivat MATLABissa alkioittain, ja löytyvät loogisilla nimillä. (cos, acos, sin jne.)
Tasavälisiä pistejoukkoja luodaan komennolla linspace, tai vaihtoehtoisesti MATLABin kaksoispiste-notaatiolla. Tutustu kummankin dokumentaatioon, ja päätä kumpaa kannattaa tässä tilanteessa käyttää.
Huomaa, että c)-kohdassa nimittäjällä on nollakohtia.
- 12. Funktion g(x) kiintopiste on piste x0, jolle pätee g(x0) = x0. Valistuneen arvauksen kiintopisteen sijainnista voi piirtämällä kuvaajat y = g(x) ja y = x samaan kuvaan, ja arvioimalla käyrien leikkauspistettä graafisesti. Käyttämällä tätä tekniikkaa, arvioi funktion g(x) = cos(x) kiintopisteen sijaintia. Vihje: Kaksi käyrää voidaan piirtää samaan kuvaan joko yhdellä plot käskyllä : plot(x1,y1,x2,y2), tai vaihtoehtoisesti voidaan käyttää MATLABin hold optiota:plot(x1,y1);
hold on
plot(x2,y2);
hold off - 13. Piirrä MATLABilla alla oleva kuva.
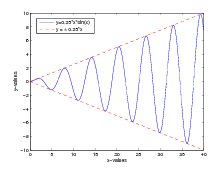 Vihje: Selityslaatikko luodaan komennolla legend, akselikuvaukset komennoilla xlabel ja ylabel.
Vihje: Selityslaatikko luodaan komennolla legend, akselikuvaukset komennoilla xlabel ja ylabel.
- 14. Tässä tehtävässä tutkitaan kuvien, matriisien ja singulaariarvojen yhteyksiä.
Matriisin A ∈ ℝm×n singulaariarvohajotelma on
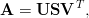
missä matriisi S on diagonaalimatriisi, ja matriisit U ja V ovat ortogonaalisia neliömatriiseja. Matriisin sisältämää informaatiota voidaan tietyssä mielessä kompressoida tiputtamalla osia singulaariarvohajotelmasta pois; on todistettavissa että (MATLABilla ilmaistuna) U(:,1:k)*S(1:k,1:k)*V(:,1:k)’ on paras mahdollinen rank(k)-approksimaatio matriisille A.
Kuva voidaan ajatella m × n matriisina, missä i,j alkio ilmaisee vastaavassa paikassa olevan pikselin väriarvon. Tutkitaan sitten kuinka singulaariarvoja voidaan käyttää hyväksi kuvien pakkaamisessa ja hahmontunnistuksessa.
Lue haluamasi kuva sisään MATLABin imread komennolla. Komento luo (yleensä, mutta hieman kuvasta riippuen), m × n × 3 matriisin. Tämä vastaa RGB-esitystä: ensimmäisessä kerroksessa on punaisen värin intensiteetit, toisessa vihreän ja kolmannessa sinisen. Muuta tämä matriisi harmaaskaalaan komennolla rgb2gray. Tämän jälkeen tee matriisille singulaariarvohajotelma komennolla [u s v] = svd(P), missä P on kuvasi matriisiesitys. Tutki sitten millä k:n arvolla komentojono
>> M = u(:,1:k)*s(1:k,1:k)*v(:,1:k)’;
>> image(M)tuottaa havaittavia tuloksia. Pitäisi myös päteä, että kuvan isommat hahmot alkavat erottua ensin, mikä tekee singulaariarvoista huomattavan tehokkaan työkalun hahmontunnistuksessa. Vihje: Kuvan ulottuvuuksien ei kannata olla kovin isoja: singulaariarvohajotelma on raskas laskettava. Jos haluat lisähaastetta, erottele kuvan värikerrokset, tee hajotelma niille erikseen, ja kokoa tulokset. Näin saat aikaan värikuvia.
- 15. Piirrä
- 1.
- xe−x2 välillä
![[− 2,2]](matlabHarGrafiikka15x.png)
- 2.
- 1∕(1 + x2) välillä
![[− 4,4 ]](matlabHarGrafiikka16x.png)
Vihje: Muista pisteet laskutoimituksissa!
- 16. Luo n × n matriiseja A jollakin sopivalla n (s.o. enemmän kuin kymmenen, vähemmän kuin sata), joiden alkiot ovat muotoa
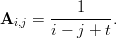
Piirrä matriisin A ominaisarvot tasoon, kun t vaihtelee välillä [−1, 1]. Mitä havaitset? Voisivatko perättäisten ominaisarvojen radat esittää jotain? Vihje: Mieti miten matriisin voisi määritellä ilman silmukkaa. Matriisin ominaisarvot lasketaan komennolla eig – huomaa, että jos matriisi on kovin iso, niin laskeminen voi kestää kauan.
- 17. HT
a) Piirrä funktiot cos t ja sin t samaan kuvaan eri väreillä.
b) Piirrä toiseen kuvaan yksikköympyrä ja säännöllinen n−kulmio esim. arvolla n = 10. Järjestä sopivilla axis-komennoilla skaalat yhtäsuuriksi, jotta ympyrä näkyy ympyränä.
c) Piirrä yksikköympyrän kuva joillain edellä esiintyneillä lineaarikuvauksilla(tai muilla keksimilläsi).
Vihje: Uusi grafiikkaikkuna: figure
Muistathan ympyrän luonnollisen parametriesityksen.
Ympyrän data koostuu oikeasti säännöllisesen n-kulmion nurkkapisteistä, missä esim. n = 100 (linspace:n oletus). Ympyrän kuvan piirtäminen on siten sama homma kuin edellisissä lineaarikuvaustehtävissä. - 18. Matlab ja Maple (tee molemmilla).
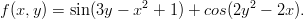
Piirrä pintakuva ja korkeuskäyräpiirros.
Ota alueeksi vaikka [-2 2 -1 1] .
Vihje: Tutustu samalla Matlabin meshgrid:n toimintaan.
Korkeusarvomatriisi Z tehdään kahden muuttujan funktiolle tähän tapaan:>> x=linspace(a,b,m); y=linspace(c,d,n); % m ja n luokkaa 30.
>> [X,Y]=meshgrid(x,y);
>> Z=f(X,Y);(Kokeile periaatetta pienillä, hiukan erikokoisilla matriiseilla X,Y.)
Tässä funktion f on toimittava pisteittäisin operaatioin. Jos vaikka f(x,y) = x2 −y2, kirjoitettaisiin: Z=X.^2 - Y.^2;Pintoihin mesh(x,y,Z), surf(x,y,Z), ... Kokeile myös colorbar yms.
Matlabilla korkeuskäyriin contour , voit myös kokeilla ezcontour-funktiota. Mahdollisuus on kokeilla myös korkeuskäyrien valitsemistapoja, clabel.
Älä diskretoi liian hienoksi. Linspacessa 100 on ihan liikaa, n. luokkaa 30 olkoon lähtökohta.
Maple: Helpompaa, mutta tulos ei aivan niin loistava kuin Matlabissa. (Osin tosin varsin hienoa tämäkin, ja “context sensitive”).
> with(plots):
> plot3d(f(x,y),x=a..b,y=c..d);
> contour(f(x,y),x=a..b,y=c..d); # Tarkista! - 19. Piirrä sin(2x) sinisellä ja cos(5x) punaisella, välillä [−π,π] (samaan kuvaan). Merkitse vielä samaan kuvaan sin(2x):n arvot o-merkeillä x-pisteissä
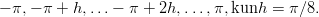
Vihje: Pane merkille tällaiset grafiikan ulkoasua säätelevät lisäkomennot (jotka voidaan antaa jälkikäteen (paitsi hold on pitää antaa ajoissa)):
grid on/off, hold on/off, axis, xlim, ylim, figure, subplot, shg , close all Tutki toiminta help:stä ja oppaista. Aloita: help plot (tai klikkaa: plot). Suorita joitakin kokeiluja (mutta älä uuvuksiin asti tässä vaiheessa vielä). - 20. Piirrä samaan kuvaan funktioiden sin kx kuvaajat välillä
![[0,2π ]](matlabHarGrafiikka20x.png) , kun k = 1…5.
, kun k = 1…5.
- 1.
- Tee nuolinäppäintä ( ↑ ) komentoeditoinnissa hyödyntäen ja hold on- komentoa käyttäen.
- 2.
- Kirjoita pieni for-silmukka.
- 3.
- Muodosta 5-sarakkeinen matriisi, jonka k : s sarake on sin kx, missä x on “x-vektori” .
Vihje: Muodosta ensin 100 × 5-matriisi , jonka sarakkeet ovat kx, k = 1…5. Kätevimmin matriisikertolaskulla x*K, missä x on (100-pituinen) sarakevektori ja K (5-pituinen) indeksi(rivi)vektori. Mieti huolellisesti, miksi!
Toinen mahdollisuus on käyttää meshgrid-komentoa, jonka käyttöön rutinoidutaan 3d-grafiikan yhteydessä. - 21. Matriisiin sovellettuna plot-funktio piirtää kunkin matriisin sarakkeen. Varsin käyttökelpoinen muoto on plot(x,A), jossa x on A:n sarakkeiden pituinen argumenttivektori.
Suorita seuraavat komennot:
>> x=linspace(-1,1);
>> V=vander(x);
>> plot(x,V); shgJatka tähän tapaan:
>> figure % Avaa uusi grafiikkaikkuna.
>> V=fliplr(V);
>> W=V(:,1:10);
>> plot(x,W);shgSelitä, mitä näissä tapahtuu.
- 22. Piirrä samaan kuvaan potenssit x,x2,…,xn, missä n on muuteltava parametri. Käytä m-tiedostoa (skriptiä) seuraavan ohjeen mukaisesti.
Avaa uusi m-tiedosto ( FILE-valikosta open->new->script ) ja talleta se vaikkapa nimelle potenssipiirto.m .
Tai kirjoita komentoikkunassa: >> edit ’potenssipiirto.m’
Aloita tiedosto jotenkin näin:% % Piirret“”a“”an potenssifunktioita.
% Tiedosto: potenssipiirto.m.
% Laatinut Vilja Varis 1.1.2012 % HUOM! ellet muuta tätä, saat 0 pistettä!
close all % Grafiikkaruudun tyhjennys
n=5; % Muuteltava parametri
...Talleta ja kirjoita komentoikkunaan:
>> potenssipiirto
Tällöin tiedostossa olevat Matlab-komennot suorittuvat.
Komennot suorittuvat myös editori-ikkunasta CTR-ENTER :llä. (Mac:ssä yleisesti CTR:n sijasta cmd.)
(Vihreä nuoli tai F5 toimivat myös.)
Suorita skripti muutamalla eri n:n arvollaVihje:
- 1.
- Tee for-silmukka ja käytä hold on-komentoa uuden kuvan piirtämiseksi vanhan kaveriksi.
- 2.
- Olkoon aluksi vaikka n = 3,m = 7, missä m on x-vektorin pituus. Muodosta matriisit
N ja X, missä N koostuu vakiosarakkeista 1,2,3 ja X saadaan latomalla kolme x-saraketta
rinnakkain. Tällöin X.^N on matriisi, jonka sarakkeina ovat x-vektorin potenssit 1,2,3.
Kuva saadaan nyt komennolla plot(x,X.^N). (Yleisesti: plot(x,Y) piirtää kunkin
Y-matriisin sarakkeen x:n toimiessa x-akselina, kun x on Y:n sarakkeiden pituinen vektori.
(Toimii myös riveittäin, jos x on rivien pituinen.)
Miten saadaan helpoimmin matriisit X, N ? Standarditapa on tämä:
>> nind=1:3;
>> [N,X]=meshgrid(nind,x);Suorita ja selvitä itsellesi.
Tee sitten esim. 100-pituinen x-vektori ja vaihtele myös n:ää ja piirrä sileitä kuvia.
Lopuksi voit kokeilla, miltä näyttää mesh(nind,x,X.^N) .Huom! Tällainen meshgrid-komennon käyttö on rutiinitoimenpide 3d-grafiikan tekemisessä, sen toimintaperiaate on mukava ymmärtää, sitä tämä yrittää palvella.
- 3.
- Helpoin tapa lienee Vandermonden matriisi vander. Siitäpä on eri tehtävä (05), mutta ei ole huonoa harjoitella tässäkin uudestaan.
- 23.
[3D-grafiikkaa, korkeuskäyriä] HA
Olkoon
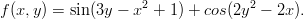
Piirrä pintakuva ja korkeuskäyräpiirros, jälkimmäinen sekä contour että ezcontour-funktioilla. Tässä on mahdollisuus kokeilla korkeuskäyrien valitsemistapoja, myös clabel. Ota alueeksi vaikka [-2 2 -1 1] .
Vihje: Opiskele:
http://math.tkk.fi/˜apiola/matlab/opas/lyhyt/grafiikka.html#sec:3d
Matlab-help: doc mesh, doc surf, doc contour______________________________________Ratkaisu: ./mlG07ratk.m
./html/mlG07ratk.html
http://math.tkk.fi/˜apiola/matlab/opas/lyhyt/ratkaisuja/html/H3teht4.html - 24. Olkoon
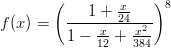
Tämä on exp-funktion rationaaliapproksimaatio, ns. Pade-approksimaatio. Piirrä kuvaaja välillä [0,4].
Piirrä samaan kuvaan exp-funktio eri värillä ja eri kuvaan erotus f(x) −exp(x) Aloita vaikka: x=linspace(0,4,200);Vihje: Tehtävässä harjoitellaan lausekkeen muodostamista pisteittäisin laskutoimituksin.
Homma selkeytyy jakamalla pienempiin osiin, ainakin nyt tällaisiin:>> x=...;
>> osoittaja=...;
>> nimittaja=...;
>> f=...; % Huomaa: f on muuttuja (200-pituinen vektori), ei funktio.
>> % Tässä ei siten saa kirjoittaa: f(x) = ..._________________________________________________________________________________
Ratkaisu:
>> x=linspace(0,4,200);
>> osoittaja=1+x/24; % Skalaarilla jaossa ei tarvia pistettä.
>> % (Jos skalaari jaettaisiin vektorilla, niin toki tarvittaisiin.)
>> nimittaja=1-x/12+x.^2/384;
>> f=(osoittaja./nimittaja).^8;
>> plot(x,f)
>> hold on
>> plot(x,exp(x),’r’)
>> figure % uusi graiikkaikkuna
>> plot(x,f-exp(x))Opettajalle: Tästä voisi tehdä jatkotehtävän tyyppiä: Vertaa Taylorin sarjaa ja Pade-approksimaatiota. Ja vielä: voisi vaikka opettaa, miten Pade-approksimaatioita muodostetaan.
- 25. Olkoot c ja z0 kompleksilukuja. Tällöin rekursion
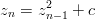
määräämä dynaaminen systeemi tunnetaan kvadraattisena kuvauksena. Valituille luvuille c ja z0 ylläoleva rekursio johtaa kompleksiseen lukujonoon z1,z2,z3…. Tätä jonoa kutsutaan z0:n kiertoradaksi. Riippuen lukujen c ja z0 valinnasta ratojen muotoja on useita.
Annetulle kiinteälle luvulle c useimmilla z0 rata lähestyy ääretöntä (eli |zn| kasvaa rajatta kun n →∞.) Joillakin c ja z0 rata kuitenkin suppenee kohti jotain periodista silmukkaa (eli arvot kiertävät z0 jollain tietyllä etäisyydellä |zn|); joillakin alkuarvoilla rata on kaoottinen. Nämä alkuarvot z0 ovat kuvauksen Julia-joukko.
Tässä harjoituksessa kirjoitetaan MATLAB-ohjelma, joka laskee ns. täytetyn Julia-joukon, joka koostuu niistä alkioista z0 joiden radat jollain annetulla arvolla c eivät kasva rajatta – tavallinen Julia-joukko on tämän joukon reuna.
On näytetty, että jos |zn| kasvaa isommaksi kuin 2 jollain arvolla n, rekursio kasvaa rajatta. Arvoa n jolla tämä tapahtuu, kutsutaan tässä tehtävässä pisteen z0 ”pakonopeudeksi.”
Aloita kirjoittamalla funktio n = escapeVelocity(z0,c,N), jossa N on jokin yläraja pakonopeuksille (erityisesti: jos |zn| < 2∀n < N, funktion tulee palauttaa N. Näin vältetään ikuiset silmukat).
Luodaksesi Julia-joukon kirjoita funktio M=julia(zMax,c,N). Argumentti zMax määrää kompleksitasosta nelikulmion |Im(z)| < zmax,|Re(z)| < zmaz. c ja N ovat samat argumentit kuin edellä, palautettava matriisi M koostuu määritetyn hilan pakonopeuksista.
Aloita funktion julia kirjoittaminen määrittelemällä 500 × 500 hila realitasossa, luo sen avulla vastaava hila Z kompleksitasolle, ja aja funktio escapeVelocity jokaiselle matriisin Z alkiolle. Vihje: Realiakselin väli [a,b] määritellään MATLABissa komennolla I = linspace(a,b,n), missä n on haluttujen pisteiden määrä, kuten esim. 500. Hila reaalitasolle määritellään komennolla [x y] = meshgrid(t1,t2) , missä t1 ja t2 ovat välejä reaaliakselilta. Tästä luodaan kompleksitasoa peittävä hila komennolla z = x+i*y.
Kompleksiluvun modulin saa selville itseisarvofunktiolla abs.
- 26. Kirjoita MATLAB-skripti, joka laskee ja piirtää seuraavat funktiot:
- a)
- y = 5 cos(3πx). Laske arvo 101:ssä tasavälisessä pisteessä välillä 0 ≤ x ≤
1.
- b)
- y =
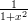 välillä −5 ≤ x ≤ 5 .
välillä −5 ≤ x ≤ 5 .
- c)
- y =
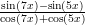 . Laske arvo 200 tasavälisessä pisteessä välillä −
. Laske arvo 200 tasavälisessä pisteessä välillä −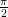 ≤
x ≤
≤
x ≤ 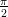 . Käytä axis komentoa asettaaksesi näytettävät akselit väleille
−2 ≤ x ≤ 2 ja −10 ≤ x ≤ 10.
. Käytä axis komentoa asettaaksesi näytettävät akselit väleille
−2 ≤ x ≤ 2 ja −10 ≤ x ≤ 10.
Trigonometriset funktiot toimivat MATLABissa alkioittain, ja löytyvät loogisilla nimillä. (cos, acos, sin jne.)
Tasavälisiä pistejoukkoja luodaan komennolla linspace, tai vaihtoehtoisesti MATLABin kaksoispiste-notaatiolla. Tutustu kummankin dokumentaatioon, ja päätä kumpaa kannattaa tässä tilanteessa käyttää.
- 27. Funktion g(x) kiintopiste on piste x0, jolle pätee g(x0) = x0. Valistuneen arvauksen kiintopisteen sijainnista voi piirtämällä kuvaajat y = g(x) ja y = x samaan kuvaan, ja arvioimalla käyrien leikkauspistettä graafisesti. Käyttämällä tätä tekniikkaa, arvioi funktion g(x) = cos(x) kiintopisteen sijaintia. Vihje: Kaksi käyrää voidaan piirtää samaan kuvaan joko yhdellä plot käskyllä : plot(x1,y1,x2,y2), tai vaihtoehtoisesti voidaan käyttää MATLABin hold optiota:plot(x1,y1);
hold on
plot(x2,y2);
hold off - 28. Piirrä MATLABilla alla oleva kuva. Vihje: Selityslaatikko luodaan komennolla legend, akselikuvaukset komennoilla xlabel ja ylabel.
- 29. Tässä tehtävässä tutkitaan kuvien, matriisien ja singulaariarvojen yhteyksiä.
Matriisin A ∈ ℝm×n singulaariarvohajotelma on
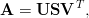
missä matriisi S on diagonaalimatriisi, ja matriisit U ja V ovat ortogonaalisia neliömatriiseja. Matriisin sisältämää informaatiota voidaan tietyssä mielessä kompressoida tiputtamalla osia singulaariarvohajotelmasta pois; on todistettavissa että (MATLABilla ilmaistuna) U(:,1:k)*S(1:k,1:k)*V(:,1:k)’ on paras mahdollinen rank(k)-approksimaatio matriisille A.
Kuva voidaan ajatella m × n matriisina, missä i,j alkio ilmaisee vastaavassa paikassa olevan pikselin väriarvon. Tutkitaan sitten kuinka singulaariarvoja voidaan käyttää hyväksi kuvien pakkaamisessa ja hahmontunnistuksessa.
Lue haluamasi kuva sisään MATLABin imread komennolla. Komento luo (yleensä, mutta hieman kuvasta riippuen), m × n × 3 matriisin. Tämä vastaa RGB-esitystä: ensimmäisessä kerroksessa on punaisen värin intensiteetit, toisessa vihreän ja kolmannessa sinisen. Muuta tämä matriisi harmaaskaalaan komennolla rgb2gray. Tämän jälkeen tee matriisille singulaariarvohajotelma komennolla [u s v] = svd(P), missä P on kuvasi matriisiesitys. Tutki sitten millä k:n arvolla komentojono
>> M = u(:,1:k)*s(1:k,1:k)*v(:,1:k)’;
>> image(M)tuottaa havaittavia tuloksia. Pitäisi myös päteä, että kuvan isommat hahmot alkavat erottua ensin, mikä tekee singulaariarvoista huomattavan tehokkaan työkalun hahmontunnistuksessa. Vihje: Kuvan ulottuvuuksien ei kannata olla kovin isoja: singulaariarvohajotelma on raskas laskettava. Jos haluat lisähaastetta, erottele kuvan värikerrokset, tee hajotelma niille erikseen, ja kokoa tulokset. Näin saat aikaan värikuvia.
- 30. Luo n × n matriiseja A jollakin sopivalla n (s.o. enemmän kuin kymmenen, vähemmän kuin sata), joiden alkiot ovat muotoa
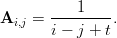
Piirrä matriisin A ominaisarvot tasoon, kun t vaihtelee välillä [−1, 1]. Mitä havaitset? Voisivatko perättäisten ominaisarvojen radat esittää jotain? Vihje: Mieti miten matriisin voisi määritellä ilman silmukkaa. Matriisin ominaisarvot lasketaan komennolla eig – huomaa, että jos matriisi on kovin iso, niin laskeminen voi kestää kauan.
- 31. HT
a) Piirrä funktiot cos t ja sin t samaan kuvaan eri väreillä.
b) Piirrä toiseen kuvaan yksikköympyrä ja säännöllinen n−kulmio esim. arvolla n = 10. Järjestä sopivilla axis-komennoilla skaalat yhtäsuuriksi, jotta ympyrä näkyy ympyränä.
c) Piirrä yksikköympyrän kuva joillain edellä esiintyneillä lineaarikuvauksilla(tai muilla keksimilläsi).
Vihje: Uusi grafiikkaikkuna: figure
Muistathan ympyrän luonnollisen parametriesityksen.
Ympyrän data koostuu oikeasti säännöllisesen n-kulmion nurkkapisteistä, missä esim. n = 100 (linspace:n oletus). Ympyrän kuvan piirtäminen on siten sama homma kuin edellisissä lineaarikuvaustehtävissä. - 32. Matlab ja Maple (tee molemmilla).
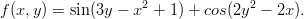
Piirrä pintakuva ja korkeuskäyräpiirros.
Ota alueeksi vaikka [-2 2 -1 1] .
Vihje: Tutustu samalla Matlabin meshgrid:n toimintaan.
Korkeusarvomatriisi Z tehdään kahden muuttujan funktiolle tähän tapaan:>> x=linspace(a,b,m); y=linspace(c,d,n); % m ja n luokkaa 30.
>> [X,Y]=meshgrid(x,y);
>> Z=f(X,Y);(Kokeile periaatetta pienillä, hiukan erikokoisilla matriiseilla X,Y.)
Tässä funktion f on toimittava pisteittäisin operaatioin. Jos vaikka f(x,y) = x2 −y2, kirjoitettaisiin: Z=X.^2 - Y.^2;Pintoihin mesh(x,y,Z), surf(x,y,Z), ... Kokeile myös colorbar yms.
Matlabilla korkeuskäyriin contour , voit myös kokeilla ezcontour-funktiota. Mahdollisuus on kokeilla myös korkeuskäyrien valitsemistapoja, clabel.
Älä diskretoi liian hienoksi. Linspacessa 100 on ihan liikaa, n. luokkaa 30 olkoon lähtökohta.
Maple: Helpompaa, mutta tulos ei aivan niin loistava kuin Matlabissa. (Osin tosin varsin hienoa tämäkin, ja “context sensitive”).
> with(plots):
> plot3d(f(x,y),x=a..b,y=c..d);
> contour(f(x,y),x=a..b,y=c..d); # Tarkista!
