
| Menu: |
| Etusivu |
| MattieO-materiaaliportaali |
| MATLAB |
| Maple |
| Mathematica |
Tehtäviä käyrän sovittamiseen MATLABissa.
Käytön idea: kun löydät mieleisesi tehtävän, sen alapuolella on linkki tex-tiedostoon. Lataa tiedosto, ja liitä se pääsivulta löytyvään harjoituspohjaan.
- 1. mlCF01.tex [Maple: ../../mplteht/mplCurveFit/mplCF01.tex]
Hermiten interpolaatio: Interpolaatioehdoissa esiintyy myös derivaattoja.
Opettajalle: Tehtävän alkuperäinen tarkoitus on demonstroida luontevaa, nautittavaa Maple-työskentelyä. Sopii myös oikein hyvin Matlab-tehtäväksi. Matlabissa on valmiina polyder-funktio, jonka ohjelmointi on sinänsä myös oikein sopiva pikku harjoitustehtävä. Tässä tehtävässä ei ole tarvetta/syytä käyttää symbolic toolboxia.
Määritä 4. asteen polynomi p, joka toteuttaa ehdot:
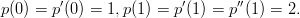
(a) Käsittele polynomi lausekkeena.
Tarkista tulos sopivasti subs-komennoilla ja piirrä kuva/kuvia polynomista ja derivaatoista.(b) Käsittele polynomi funktiona.
Huom: 5 ehtoa ja 5 tuntematonta kerrointa ⇒ järkevän tuntuinen tehtävä. Yleisesti “järkevälläkään” Hermiten interpolaatiotehtävällä ei aina ole yksikäsitteistä ratkaisua (kuten ei neliömatriisin määräämällä lineaarisella yhtälöryhmälläkään – siitähän on kyse). Pelkkiä funktion arvoja koskevalla interpolaatiotehtävällä aina on (koska “Vandermonden neliömatriisi” on aina ei-singulaarinen).
Tässä opetellaan erityisesti Maplen kätevää ratkaisutekniikkaa. Vihje: Kirjoita polynomi lausekkeeksi tyyliin:p:=a*x^4+b*x^3 + .... ,
missä a,b,…,e ovat määrättävät kertoimet.Derivaatta: diff
Arvojen (x=0,x=1) sijoittaminen p:n lausekkeeseen: subs
Yhtälön ratkaiseminen: solveKaikista saat tietoa näin ?diff, ...
- 2. Oletetaan, että meille on annettu dataa muodossa (xk,yk).k = 1…m, johon muodustuu kaksi murtopisteen erottamaa lineaarista suuntausta. Esimerkiksix=-2:0.1:4; y=0.2*sin(3*x);
y(x¡1)=y(x¡1)+0.5*(x(x¡1)-1);
y(x>=1)=y(x>=1)+2*(x(x>=1)-1);muodostaa selvän murtopisteen kohtaan x = 1. Intuitiivisesti tuntuu selvältä, että tällaiseen dataan kannattaa sovittaa PNS-suoran sijaan paloittain lineaarinen funktio, ts. ”suora murtopisteellä.”
Kirjoita ohjelma joka tekee tämän: ohjelman tulee valita murtopiste (s,t) tasosta hiiren klikkauksen perusteella (kts. vihje) ja sovittaa paloittain lineaarisen funktion dataan tätä murtopistettä käyttäen, ts. sovittaa suoran
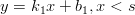
pisteisiin (xk,yk),xk < s ja suoran
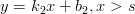
pisteisiin (xk,yk),xk > s. Vihje: Tehtävän keskeinen osa on murtopisteen valinta ja datapisteiden suodatus.
Murtopisteen valintaan kannattaa käyttää ginput funktiota, joka valitsee klikatun pisteen kuvasta tyyliin
[x y] = ginput(1);Datan suodatukseen kannattaa käyttää MATLABin loogista indeksöintiä: esimerkiksi valitaan kaikki vektorin pisteet, jotka ovat pienempiä kuin 5.
a = b(b¡5); - 3. mlCF02.tex
Muodosta interpolaatiopolynomi pisteistölle, joka saadaan laskemalla funktion f(x) = cos(1 + x2) arvot tasavälisessä x-pisteistössä, jossa on 7 pistettä välillä [0, 3]. Piirrä samaan kuvaan funktio, datapisteet (rinkuloilla) ja interpolaatiopolynomi.Vihje: help(doc) polyfit, polyval .
Sinun on tiedettävä, mikä on polynomin asteluku.
Tarkistus: Kulkeeko polynomi kaikkien datapisteiden kautta. - 4. Kirjoita funktio, jonka otsikko ja “help-kommentit” voisivat olla:function [kertoimet,condnr]=vandinterp(xdata,ydata)
% Funktio laskee interpolaatiopolynomin kertoimet Vandermonden
% systeemin ratkaisulla ja palauttaa my“”os cond-luvun.
% Esim:
% xdata=0:5; ydata=xdata.*sin(xdata);
% [c,cnr]=vandinterp(xdata,ydata);
Laske vaikkapa kommenttiesimerkin tapaus ja vertaa polyfit-funktion antamiin kertoimiin. Piirrä data ja interpolaatiopolynomi. Käytä arvojen laskentaan polyval-funktiota.
Vihje: Olkoon p(x) = a0 + a1x + … + anxn etsitty polynomi.
Määrätään tuntemattomat kertoimet interpolaatioehtojen p(xk) = yk,k = x0,…xn avulla saatavasta lineaarisesta yhtälösysteemistä ratkaisemalla.
Kirjoita yhtälöryhmä tässä yleisessä muodossa ja tee ensin Matlab-skripti tyyliinxd=...;
yd=...;
A=...; % Yht.ryhman matriisi, help/doc vander
a= % Ratkaisuna saatava kerroinvektori, help slash (a=A“...)d
x=linspace(alkup,loppup); % x-pisteet piirt. varten
y=polyval(...); % Polynomin arvot x-pisteissa
...
plot(xd,yd,’o’)
hold on
plot(x,y)
grid onTarkistus: Kulkeeko polynomi kaikkien datapisteiden kautta.
Kun skripti toimii, tee sen pohjalta pyydetty funktio. Sovella funktiotasi johonkin tämän tehtäväkokoelman interpolaatiotehtävään. - 5. Eräs kemiallinen koe tuotti seuraavat datapisteet:tdata=[-1 -0.960 -0.86 -0.79 0.22 0.5 0.93]; % Aikapisteet
ydata= [ -1 -0.151 0.894 0.986 0.895 0.5 -0.306]; % ReaktiotuloksetTarkoitus on estimoida reaktiotulosfunktion y(t) arvoja välillä
![[− 1,1]](matlabHarCurveFit3x.png)
- 1.
- Piirrä datapisteet.
- 2.
- Muodosta interpolaatiopolynomi ja piirrä samaan kuvaan.
- 3.
- Muodosta asteita 2,3,4 olevat PNS-polynomit ja piirrä samaan kuvaan
- 4.
- Sovita vielä splini ja piirrä samaan.
- 5.
- Asettele grafiikkaikkuna paremmaksi vaikka tyyliin:
a=min(xdata)-0.1;b=max(xdata)+0.1;
c=min(ydata)-0.1;d=max(ydata)+0.1;
axis([a b c d])Käytä myös legend-komentoa ja kokeile grid on
Vihje:
Ratkaisu:mlCF04ratk.m [Tulee, numero?]
- 6.
- a)
- Piirrä suorat y = 0.2 − 0.5x,y = 0.2 + 2x,y = −0.3 + 1.5x ja y = 0.95x.
- b)
- Kirjoita suorat yhtälöA[x; y] = b PNS-mielessä, ja piirrä ratkaisu samaan kuvaan suorien kanssa.
- 7. mlCF07.tex/mplCF07.tex // Matlab,Maple,[Mathematica]
W.A Mozartin(1756-1791) sävellyksiä indeksoidaan Köchel-luvuilla, jotka ilmaisevat teosten sävellysjärjestyksen. Alla on eräitä Köchel-lukuja, ja vastaavien teosten sävellysvuosia.
Number Year
1 1761
75 1771
155 1772
219 1775
271 1777
351 1780
425 1782
503 1786
575 1789
626 1791Käyttäen tätä dataa, arvioi teoksen Sinfonia Concertanten sävellysvuosi, kun tiedetään, että sen Köchel-numero on 364. Vihje: Piirrä ensin datapisteet tasoon, ja päätä millaista menetelmää kannattaa käyttää. Epäilemättä sopivan asteista PNS-polynomia. Suorita joitakin sovituksia, ja tarkista sitten tulos vaikka Wikipediasta.
- 8.
- a)
- Luo dataa seuraavalla skriptillä:
r = 0.5+0.5*rand(10,1);
theta =2*pi*rand(10,1)
x = 3*r.*cos(theta);
y = 3*r.*sin(theta);ja piirrä data pisteittäin.
- b)
- Sovitamme dataan ympyrän muotoa (x − c1)2 + (y − c
2)2 = r2. Ympyrän
sovituksessa etsitään kahta arvoa: ympyrän keskipistettä (c1,c2),
ja sen sädettä r. Helpoimmin sovitus onnistuu huomaamalla, että
(x − c1)2 + (y − c
2)2 = r2 ⇔ 2xc
1 + 2yc2 + (r2 − c
12 − c
22) = x2 + y2. Asettamalla
c3 = r2 − c
12 − c
22, saadaan yhtälö muotoa
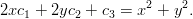
- 9. mlCF091.tex [vrt. mlCF09.tex]
- a)
- Luo dataa seuraavalla skriptillä:
n=10;
rd = 0.5+0.5*rand(n,1);
theta =2*pi*rand(n,1)
xd = 3*rd.*cos(theta);
yd = 3*rd.*sin(theta);ja piirrä data pisteittäin.
- b)
- Sovitamme dataan ellipsin:
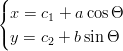
Määritä keskipiste (c1,c2) ja puoliakselit a ja b sovittamalla PNS-mielessä x:n lauseke x−dataan ja y:n lauseke y−dataan.
Piirrä data ja ellipsi ja sen keskipiste samaan kuvaan.
- c)
- Piirrä samaan kuvaan myös tehtävän mlCF09 ympyrä keskipisteineen. Ja vielä: Voit tutkia suuremmilla n:n arvoilla.
Vertailussa pitää siis tehdä data ja ajaa loppuosat skripteistä samalla datalla (tai mieluimmin edioida suoritukset peräkkäisiksi editorikappaleiksi).
- 10. Maple tai Matlab
Tutkitaan nk. Rungen ilmiötä. Laske funktion g(x) = 1∕(1 + x2) arvoja tasaisin välein väliltä [−5, 5], ja tee näihin pisteisiin perustuva polynominen interpolaatio. Piirrä sekä g(x) että P(x) samaan kuvaan. Mitä huomaat, kun valittujen datapisteiden määrää tihennetään?Kokeile interpolointia silloin, kun datapisteitä ei valita tasavälisesti, vaan ne valitaan Chebyshev-pisteiden
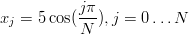
mukaan. Vihje: Polynominen interpolaatio kannattaa tehdä MATLAB-funktiolla polyfit. Funktio g kannattaa määritellä funktiokahvan avulla: g = @(x)1./(1+x.^2). Tasavälisiä pisteistä saa funktiolla linspace
Sopii aivan yhtä hyvin Maplelle.
- 11. H2T14.tex/mlCF13.tex/mplCF13.tex
Matlab,Maple,[Mathematica]Yhdysvaltojen perustuslaki vaatii, että maassa suoritetaan joka kymmenes vuosi väestönlaskenta. Ohessa on väestönlaskennan tuloksia sadoissa miljoonissa asukkaissa viime vuosisadalta.
1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 76 92 106 122 132 150 179 203 226 248
Tee polynomi-interpolointi datalle, ja ennusta väestön määrä vuonna 2010. Kuinka ennusteesi suhtautuu laskennan todelliseen tulokseen: 308,745,538 laskettua asukasta?Sovita myös eriasteisia PNS-polynomeja, vrt. Matlab Censusgui, lue Molerista: http://www.mathworks.se/moler/interp.pdfNum. Comp. with Matlab, interpolation Vihje:
- 12. mlCF15.tex [Maple: ../../mplteht/mplCurveFit/mplCF03.tex]
Opettajalle: (a)-kohta sopii ensitutustumiseen.
(b)-kohta on sikäli huono, että virhetermin suuruusluokka on toisesta maailmasta (opettavaista kylläkin, mutta alkajaisiksi vaatii ainakin varoituksen).
Lisää tehtävän opetuksia ratkaisutiedostoissa.(a) Muodosta interpolaatiopolynomi pisteistölle, joka saadaan laskemalla funktion cos(1 + x2) arvot tasavälisessä x-pisteistössä, jossa on 7 pistettä välillä [0, 3].Piirrä samaan kuvaan funktio, datapisteet ja interpolaatiopolynomi.
(b) Arvioi (Lagrangen) interpolaatiokaavan virhetermin avulla interpolaatiovirheen yläraja yo. välillä ja vertaa todelliseen.
Lause Olkoot x0,x1,…,xn erilliset pisteet ja f (n + 1) kertaa jatkuvasti derivoituva funktio xk−pisteet sisältävällä välillä. Jos pn on (1-käs) dataan (xk,f(xk)) liittyvä interpolaatiopolynomi, niin
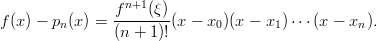
Vihje: Tässä on mahdollista harrastaa Maplen ja Matlabin yhteistyötä. Virhekaavan derivaatta muodostetaan tietysti Maplella ja lauseke sievennetään. Itse asiassa piirtämällä ja poimimalla kuvasta maksimipisteen koordinaatit, saadaan riittävän hyvä arvio.
Toinen mahdollisuus on käyttää Matlabin symbolic toolboxia.Tulotermin voisi hoitaa tehokkaimmin Matlabissa ottamalla tiheän diskretoinnin ja käyttämällä max-funktiota. Maplessakin on max-funktio, lakenta on Matlabissa tehokkaampaa.
Miten tulotermi lasketaan Matlabissa? Vaikka tähän tapaan:
1. x=linspace(....,N)
2. Tedään matriisi X, jossa x-vektoreita allekkain n+1 kpl.
3. Tehdään matriisi X0, jossa rivitx0 x0 ... x0 N kpl.
x1 x1 ... x1 N kpl.
...
xn xn ... xn N kpl.
Nämä syntyvät vaikka meshgrid-komennolla tai ulkotuloilemalla ykköspystyvektorilla.
4. Vähennetään matriisit ja prod()). Sitten vain abs ja max kehiin.Tosi Matlabmaista! (Ei moitita, vaikka tekisit for-loopin, vain 8 kertaa käydään, mutta hyvä ymmärtää Matlabin hienoa matriisiajattelua, muistiahan ei nykyisin tarvitse säästellä.)
Avainsanat: Interpolaatio, käyrän sovitus, interpolaatiovirhe, Lagrange
- 13. mlCF16.tex
Kuvitteellinen koe tuotti seuraavat tulokset. Tulosten perusteella tehtiin hypoteesi, jonka mukaan pisteet noudattelevat paloittain vakiota funktiota, jolla on yksi murtopiste, toisin sanoin, funktio, joka koostuu kahdesta vakio-osasta . Testaa hypoteesi sovittamalla paloittain vakio funktio dataan käyttämällä pienimmän neliösumman menetemää.
Vihje: Tehtävä kannattaa aloittaa graafisella tarkkailulla, ja määritellä silmämääräinen murtopiste. Tämän jälkeen on helppo muodostaa minimoitavat yhtälöt.t b 0.0 0.9 0.1 1.01 0.2 1.05 0.3 0.97 0.4 0.98 0.5 0.95 0.6 0.01 0.7 -0.1 0.8 0.02 0.9 -0.1 1.0 0.0
- 14. mlCF20.tex
Pienimmän neliösumman sovitus, PNS, LSQLineaarialgebra-osioissa on aiheesta myös joitakin perustehtäviä.
Tähän tiedostoon kootaan laskaripaperiin sopivia pikaohjeita ja mielen virkistyksiä.
- .
- ..
- ...
- 15. mlCF21.tex (Kirjasta Fröberg: Numerical Analysis 1985)
Joulukuun 1–28 päivänä 1981 aurinko laski Lund:ssa klo 15.30:n ja 15.45:n välillä seuraavan taulukon mukaisesti, missä x tarkoittaa päivää (1 ≤ x ≤ 28) ja y minuuttimäärää klo 15.30:n jälkeen, jolloin aurinko laski.x y x y
1 8 19-21 3
2 7 22-23 4
3 6 24 5
4-5 5 25 6
6-7 4 26-27 7
8-9 3 28 7
10-18 2Data voidaan esittää varsin hyvin 2. asteen polynomilla. Määritä kertoimet a0,a1,a2, piirrä data ja polynomi. Minä päivänä auringonlaskuaika saavuttaa miniminsä mallin mukaan.
