How do I count the occurrences of each element in a vector

HA 16.8.2016
I came up to such questions when working on the Hardy-Ramanjan problem:

https://math.aalto.fi/opetus/Mattie/Blogi/Matlab/html/HardyRamanujan.html

After my way of counting using sort and diff presented above, I found this discussion with variuos interesting solutions to related problems. In this "publish-worksheet" I studied and ran through many of them for my own learnig and joy.

https://se.mathworks.com/matlabcentral/answers/96504-how-can-i-count-the-occurrences-of-each-element-in-a-vector-in-matlab

Contents

Set from sequence, "unique"

Matlab has the command unique. To practice "more primitive" ways, let's use logical indexing and diff.

sequence=[1 2 2 3 3 3 4 4 4 4 11 5 5 5 5 6 7]
w=sort(sequence);
b=diff(w);
I=b~=0
I=logical([1 I])
set=w(I)

sequence =
  Columns 1 through 13
     1     2     2     3     3     3     4     4     4     4    11     5     5
  Columns 14 through 17
     5     5     6     7
I =
  Columns 1 through 13
     1     0     1     0     0     1     0     0     0     1     0     0     0
  Columns 14 through 16
     1     1     1
I =
  Columns 1 through 13
     1     1     0     1     0     0     1     0     0     0     1     0     0
  Columns 14 through 17
     0     1     1     1
set =
     1     2     3     4     5     6     7    11

unique(sequence)   % does the same

ans =
     1     2     3     4     5     6     7    11

help unique, doc unique show lots of optional uses. type unique shows the code, a lot more complicated then the above lines but of course does a lot more.

Number of duplicates in many ways:

1. Logical indexing, for-loop

x=[10 25 4 10 9 4 4]
y = zeros(size(x));
for i = 1:length(x)
y(i) = sum(x==x(i));
end
y
% This was my first attempt in HardyRamanujan.
% Inefficient if lots of data, took incredibly long when p=4.
%

x =
    10    25     4    10     9     4     4
y =
     2     1     3     2     1     3     3

2. sort, diff, logical indexing, no loops

In HardyRamanujan-ws I proceeded along theses lines, the first difference was enough.

v=[1 2 2 3 3 3 4 4 4 4 11 5 5 5 5 6 7]
w=sort(v)
I1=diff(w)

v =
  Columns 1 through 13
     1     2     2     3     3     3     4     4     4     4    11     5     5
  Columns 14 through 17
     5     5     6     7
w =
  Columns 1 through 13
     1     2     2     3     3     3     4     4     4     4     5     5     5
  Columns 14 through 17
     5     6     7    11
I1 =
  Columns 1 through 13
     1     0     1     0     0     1     0     0     0     1     0     0     0
  Columns 14 through 16
     1     1     4

pick1=logical(I1==0)
AL1dup=w(pick1)              % At least 1 duplicate
%
I2=diff(AL1dup)
pick2=logical(I2==0)
AL2dup=AL1dup(pick2)         % At least 2 duplicates
%
I3=diff(AL2dup)
pick3=logical(I3==0)
AL3dup=AL2dup(pick3)          % At least 3 duplicates

% Works, not very elegant, though

pick1 =
  Columns 1 through 13
     0     1     0     1     1     0     1     1     1     0     1     1     1
  Columns 14 through 16
     0     0     0
AL1dup =
     2     3     3     4     4     4     5     5     5
I2 =
     1     0     1     0     0     1     0     0
pick2 =
     0     1     0     1     1     0     1     1
AL2dup =
     3     4     4     5     5
I3 =
     1     0     1     0
pick3 =
     0     1     0     1
AL3dup =
     4     5

3. hist gives the data right away

[y,x]=hist(v,unique(v))
bar(x,y);shg
[x;y]
%
% Elegant

% To avoid one rare possibility, one can include an extra check:

%{
 Solution 2 (using hist()) runs into trouble if unique(x) boils down to
 one number (a scalar). Then hist() takes it as the number of bins to use,
 not a bin center. Some if/else logic would catch this. Not sure if there
 is a one line answer.
%}
ux = unique(x);
if length(ux) == 1, counts = length(x);
else counts = hist(x,ux); end
counts

y =
     1     2     3     4     4     1     1     1
x =
     1     2     3     4     5     6     7    11
ans =
     1     2     3     4     5     6     7    11
     1     2     3     4     4     1     1     1
counts =
     1     1     1     1     1     1     1     1

histc help

[N,BIN]=histc(x,unique(x))
%
% [N,BIN] = histc(X,EDGES,...) also returns an index matrix BIN.  If X is a
%    vector, N(K) = SUM(BIN==K)
[N(BIN);x]

N =
     1     1     1     1     1     1     1     1
BIN =
     1     2     3     4     5     6     7     8
ans =
     1     1     1     1     1     1     1     1
     1     2     3     4     5     6     7    11

10 appears 2 times, 25 appears once, 4 appesra 3 times, ...

4. Solution with histc

x= [1     1     1     2     4     5     5]
[a,b] = histc(x,unique(x));
y = a(b)
% Works in general, perhaps requires some more thought than hist above.

x =
     1     1     1     2     4     5     5
y =
     3     3     3     1     1     2     2

5. arrayfun, nnz

y = arrayfun(@(t)nnz(x==t), x)
%

y =
     3     3     3     1     1     2     2

6. Variant: Count the number of occurrences of each integer 1,2,...

%{
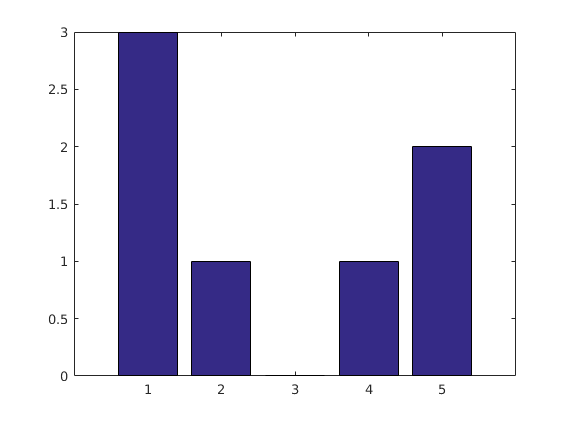
I'm working with a small variant of the original problem, where I want it
to count the number of occurrences of each whole number (till 13).
So if my input is

x = [1,1,1,2,4,5,5]

I need an output

y = [3,1,0,1,2]

How do I do this?
%}
x = [1,1,1,2,4,5,5]
y = accumarray(x(:),1)

x =
     1     1     1     2     4     5     5
y =
     3
     1
     0
     1
     2

6 b) another solution

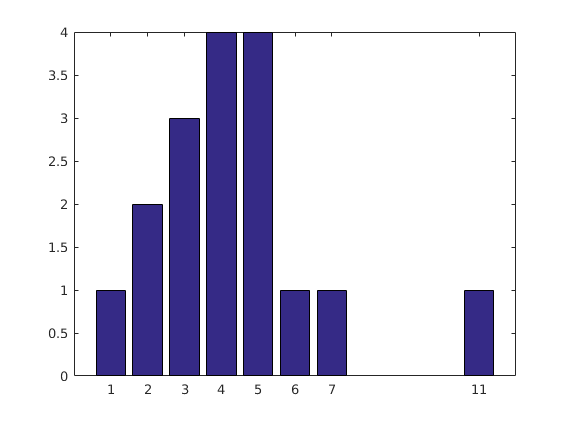
v=[1,1,1,2,4,5,5]
numbers=unique(v)      %list of elements
count=hist(v,numbers)   %provides a count of each element's occurrence
% this will give counts. and if you want to have a nice graphical
% representation then try this
bar(accumarray(v', 1))
shg
%{
Comment from the above site:

When using hist() pay attention to Dan's comment above pointing out a flaw
in the approach. This flaw is not shared by Andrei's histc approach above.
%}

v =
     1     1     1     2     4     5     5
numbers =
     1     2     4     5
count =
     3     1     1     2

Published with MATLAB® R2015b