Global minimization, 1d, assignment 4 a)
9.3.2018
Contents
Function to minimize
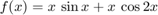
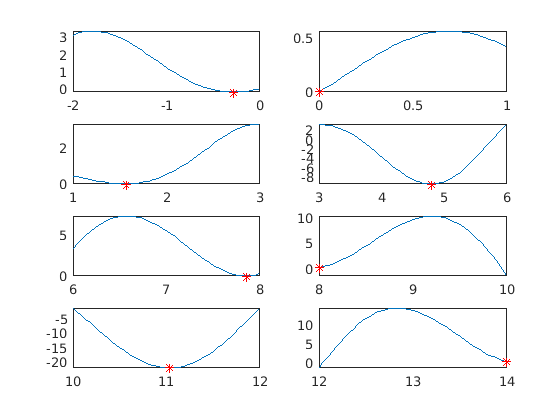
Find global minimum (and local minima) on [0,12]. Split the interval into pieces and use fminbnd on each piece. Bounds: lb = -2; ub = 14;
clear close all format compact
Define obj function
f = @(x) x.*sin(x) + x.*cos(2.*x)
f =
function_handle with value:
@(x)x.*sin(x)+x.*cos(2.*x)
Split into several parts:
lb=[-2 0 1 3 6 8 10 12]; % Lower bounds ub=[lb(2:end) 14]; % Upper bounds x0=0.5*(lb+ub); % Starting points for solver that requires them. close all
fminbnd, only bounds are needed, no starting points.
x=zeros(8,1); y=x; tic for i=1:8 [x(i),y(i)] = fminbnd(f,lb(i),ub(i)); subplot(4,2,i) fplot(f,[lb(i) ub(i)]); grid on hold on % plot(x0(i),f(x0(i)),'k+') % For solver that needs init. points. plot(x(i),f(x(i)),'ro') % Plot "labwise" minimum point (red circle) hold off %title(['Bounds: [',num2str(lb(i)),',',num2str(ub(i)),']']) end T(1)=toc minpts=[x y]
T =
0.5397
minpts =
-0.2809 -0.1599
0.0001 0.0001
1.5708 0.0000
4.7954 -9.5084
7.8540 0.0000
8.0000 0.2538
11.0318 -22.0274
14.0000 0.3923
Compare with using just Malab's vector function min.
figure tic for i=1:8 xx=linspace(lb(i),ub(i)); yy=f(xx); ymin=min(yy); Yes=(yy==ymin); % Better test: abs(yy-ymin)< tol, see later xmins{i}=xx(Yes); ymins{i}=yy(Yes); subplot(4,2,i) fplot(f,[lb(i) ub(i)]); grid on hold on plot(xmins{i},ymins{i},'ro') % Plot "labwise" minimum point (red circle) hold off end T(2)=toc xmins ymins
T =
0.5397 0.4134
xmins =
1×8 cell array
Columns 1 through 7
[-0.2828] [0] [1.5657] [4.7879] [7.8586] [10] [11.0303]
Column 8
[12]
ymins =
1×8 cell array
Columns 1 through 6
[-0.1598] [0] [6.2040e-05] [-9.5077] [2.4989e-04] [-1.3594]
Columns 7 through 8
[-22.0274] [-1.3487]
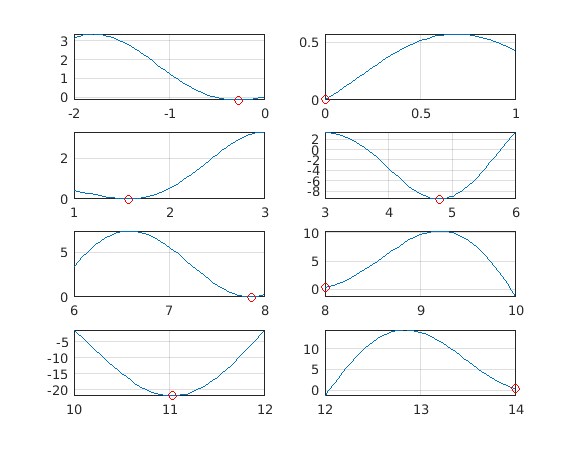
Simple vector operation was about just as fast and all results were correct, in contrary to fmincon. On "labs" 6 and 8 fmincon gets the endpoint values wrong in these cases.
If you wants to increase accuracy, you will do better by adjusting the tolerances with optimset, and running fmincon with tight intervals (obtained with logical indexing as above).
Global minimum using Matlab's [ymin,minind]=min(f(x)).
This is a couple of lines shorter than the above logical indexing way. On the other hand it misses the rest of several (almost) equal minimums. In this case works fine.
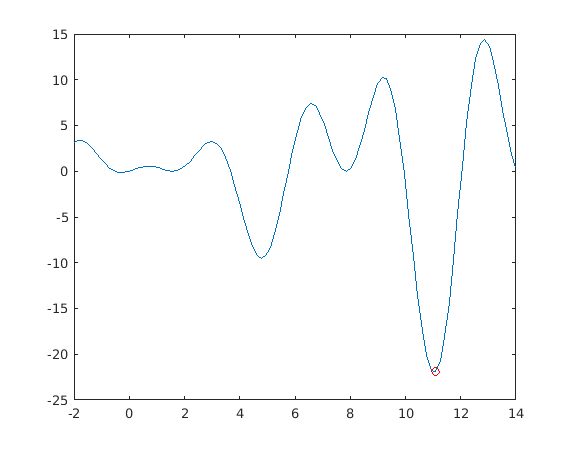
figure u=linspace(lb(1),ub(end)); [ymin,imin]=min(f(u)) % Picks first min-value and its index. plot(u,f(u),u(imin),ymin,'ro')
ymin =
-21.9305
imin =
82
%{ figure [ymin,imin]=min(f(x)) % Picks first min-value and its index. xmin=x(imin) %}
%{ figure xx=linspace(lb(1),ub(end)); plot(xx,f(xx),x,f(x),'ro') grid on %}
Task:
Enlarge interval to [-2,14] (a) Change for to parfor, run on pc and Triton, do tic - toc- timing. (b) Change to spmd, on Triton you can take more labs than 6. (c) Find max-points as well.
pc/Triton (Brute)
To use spmd, we need a form whose argument list is a 2-vector instead of two scalars.
fminbndI=@(f,Interval) fminbnd(f,Interval(1),Interval(2))
fminbndI =
function_handle with value:
@(f,Interval)fminbnd(f,Interval(1),Interval(2))
u=linspace(lb(1),ub(end)); %[ymin,imin]=min(f(u)) % Picks first min-value and its index. % plot(u,f(u),u(imin),ymin,'ro') plot(u,f(u));grid on
nlabs=2;
nlabs=8; % brute: max = 12, triton: max=24
p=parpool(nlabs);
Starting parallel pool (parpool) using the 'local' profile ... connected to 8 workers.
tic spmd % intervals=[-2 3;3 8] intervals=[lb' ub']; Int=intervals(labindex,:); [x,y]=fminbndI(f,Int); end Tspmd=toc % Varies a bit, the first is a lot slower. %{ Tspmd = 1.0614 Tspmd = 0.1692 %}
Tspmd =
1.1339
hold on for k=1:nlabs plot(x{k},y{k},'*r') end
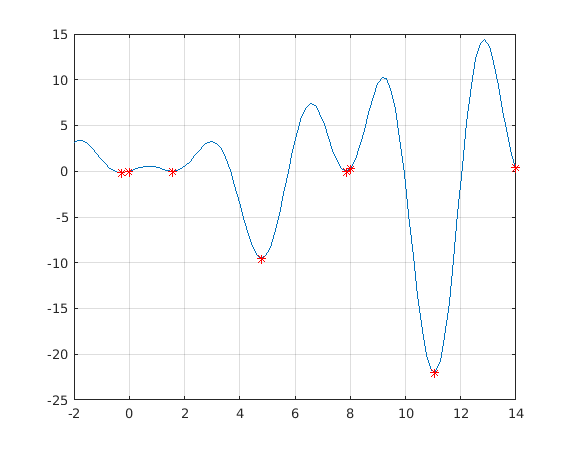
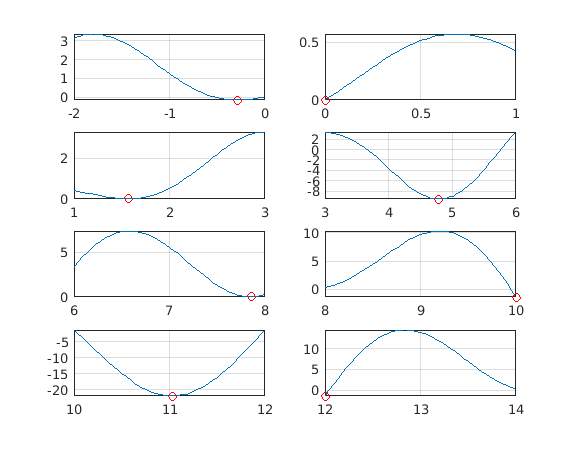
figure for k=1:nlabs subplot(4,2,k) fplot(f,[lb(k) ub(k)]) hold on plot(x{k},y{k},'*r') end