minmax2dsolver2.m

Solutions to assignment 4 (b).

Contents

close all
format compact

Unconstrained Optimization Example

Consider the problem of finding the minimum/maximum of the function:

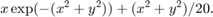
Plot the function to get an idea of where it is minimized

f = @(x,y) x.*exp(-x.^2-y.^2)+(x.^2+y.^2)/20;
fsurf(f,[-2,2],'ShowContours','on')

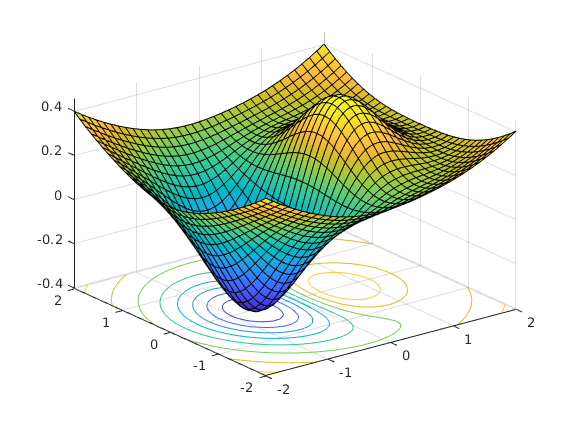
a) Just use min/max for matrix elements (no fancy methods):

tic
x=linspace(-2,2,200); y=x; % 200x200 grid
[X,Y]=meshgrid(x,y);
z=f(X,Y);
[minvala,mininda]=min(z(:));
Ta=toc
% Ta = 7.000000000000000e-04

Ta =
    0.0022

[maxvala,maxinda]=max(z(:));  % Find max as well.
minpta=[X(mininda),Y(mininda),minvala] % Use linear indexing.
maxpta=[X(maxinda),Y(maxinda),maxvala] %  --- " ---
hold on
% Mark min- and max-points in the picture:
plot3(X(mininda),Y(mininda),minvala,'.r','Markersize',20) % rotate to see
plot3(X(maxinda),Y(maxinda),maxvala,'.r','Markersize',20)
plot3(X(maxinda),Y(maxinda),-0.4,'.r','Markersize',20)  % Projection on xy-plane

minpta =
   -0.6734   -0.0101   -0.4052
maxpta =
    0.7538   -0.0101    0.4554

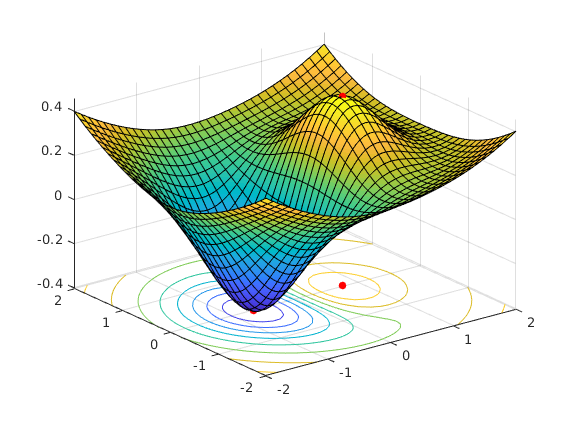
fminsearch: Matlab's optimization function

fminsearch wants fun to have one vector input instead of (x,y). (Compare with Globalmin, where we did just vice versa.)

fun = @(x) f(x(1),x(2));

Basic use of fminsearch and tic-toc-timing:

tic
x0=[0 0]  % See figure.
[xminb,fminvalb]=(fminsearch(fun,x0))
Tb=toc

x0 =
     0     0
xminb =
   -0.6690    0.0000
fminvalb =
   -0.4052
Tb =
    0.0070

max(f(x) = - min(-f(x))

[xmaxb,fmaxvalb]=(fminsearch(@(x)-fun(x),x0));fmaxvalb=-fmaxvalb

fmaxvalb =
    0.4555

Which is better?

format long
[minvala fminvalb]
[maxvala fmaxvalb]
%{
ans =
  -0.405171103703264  -0.405236869193178
ans =
   0.455427624902720   0.455466872171926
Tb =
   0.002690000000000
%}
% Accuracy slightly better with b) (fminsearch)  (5 th digit on)
% Timing better with a)
Ta_over_Tb=Ta/Tb
% ans =
%   0.266542750929368
%
% Timings vary from run to run (Ta is smaller or a lot smaller)
%

ans =
  -0.405171103703264  -0.405236869193178
ans =
   0.455427624902720   0.455466872171926
Ta_over_Tb =
   0.317122014018023

Run fminsearch with 200 x 200 = 40000 initial points.

The problem with optimization programs is the starting point. Take 40000 starting points and see how many lead (close) to min. This is a task suitable for parallel computation.

Repeat some commands from above:

%%%%%%%%%%%%% Begin copy %%%%%%%%%%%%
f = @(x,y) x.*exp(-x.^2-y.^2)+(x.^2+y.^2)/20;
x=linspace(-2,2,200); y=x; % 200x200 grid
[X,Y]=meshgrid(x,y);
z=f(X,Y);
fun = @(x) f(x(1),x(2));
%%%%%%%%%%%%%%%%% End copy %%%%%%%%%%%
tic
[m,n]=size(X);
X1=X(:);Y1=Y(:);
z=zeros(3,m*n);
for k=1:m*n
       [x,val]=(fminsearch(fun,[X1(k) Y1(k)]));
       z(:,k)=[x';val]; % k^th column:  [x(1);x(2);f(x(1),x(2))]
end
Tc=toc
% Tc = 78.3867

Tc =
  75.879069000000001

How many lead to a minimum value?

fvals=z(3,:);
minval=min(fvals)
[min(fvals) max(fvals)]

minval =
  -0.405236870252235
ans =
  -0.405236870252235   0.231461818471495

How many are close to minval?

nr_close=sum(abs(fvals-minval)<.0001)
nr_all=length(fvals)
ratio=nr_close/nr_all

nr_close =
       39994
nr_all =
       40000
ratio =
   0.999850000000000

Which are "far"?

Logindclose=abs(fvals-minval)<.0001;
Farind=~Logindclose;
%z([Farind;Farind;Farind])
x=z(1,:);y=z(2,:);mins=z(3,:);
Farpoints=[z(Farind);y(Farind);mins(Farind)]
plot3(Farpoints(1,:),Farpoints(2,:),Farpoints(3,:),'*b')

Farpoints =
  Columns 1 through 3
  -0.000005152622828  -0.405236868470644  -0.669078383945737
  -0.012968039845456   0.012968039845456  -0.010420664583319
   0.231461315085067   0.231461315085067   0.231461818471495
  Columns 4 through 6
   0.000028166297804  -0.405236870091823  -0.669064070351759
   0.010420664583319  -0.010656774944354   0.010656774944354
   0.231461818471495   0.231461775245993   0.231461775245993

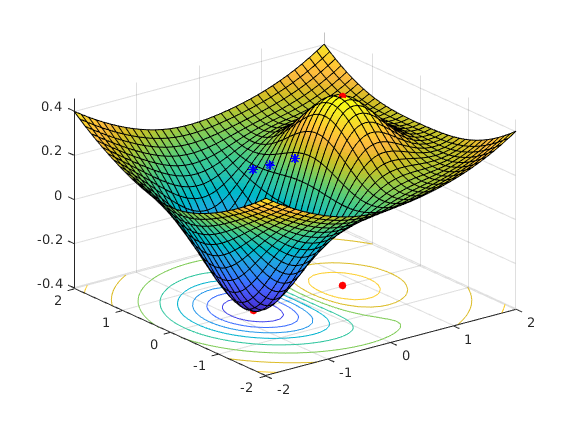
Q: Which init. pts. lead to these "far points"?

It is easy to pick those strating points, but let's leave it now.
General consideration along these lines:
"Basin of attraction", Optimization toolbox documentation.

Change for to parfor

Measure tic-toc-timing difference especially on Triton. (parfor uses all available (24) workers.)

Published with MATLAB® R2017b