minmax2dsolRosenbrock.m Rosenbrock function
Solutions to ex4, part b)
Contents
Unconstrained Optimization Example
"Classical" test function for optimization routines. Banana-shaped valley, min (1,1), value =0, steep walls, shallow bottom near min-point.
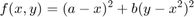
Take a=1, b=100
Plot the function to get an idea of where it is minimized
close all format compact a=1;b=100; f=@(x,y)(a-x).^2 + b*(y-x.^2).^2 fsurf(f,[-1.5,1.5 -1.5 3],'ShowContours','on') colorbar % title('f(x,y)=(a-x).^2 + b*(y-x.^2).^2, a=1,b=100') xlabel('x');ylabel('y') hold on plot3(1,1,0,'.r','MarkerSize',15)
f =
function_handle with value:
@(x,y)(a-x).^2+b*(y-x.^2).^2
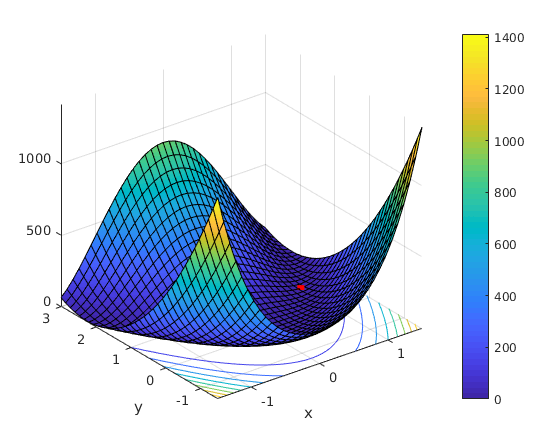
Closer to min point
figure fsurf(f,[0.5,1.5 0.5 1.5],'ShowContours','on') xlabel('x');ylabel('y') hold on plot3(1,1,0,'.r','MarkerSize',15)
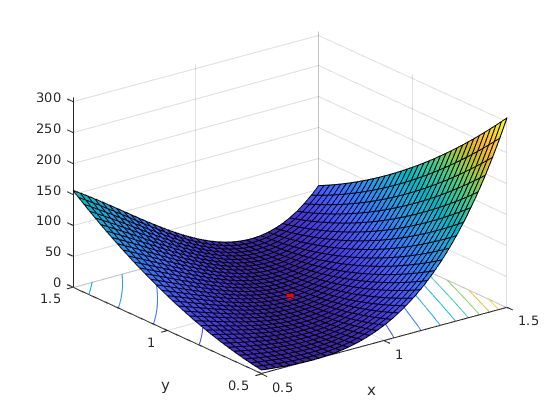
Contours
figure clf x=linspace(-1.5,1.5,200); y=linspace(-1.5,3,200); [X,Y]=meshgrid(x,y); contour(x,y,f(X,Y),60) title('f(x,y)=(a-x)^2 + b(y-x^2)^2, a=1,b=100') hold on contour(x,y,f(X,Y),[0,0.1]) grid on
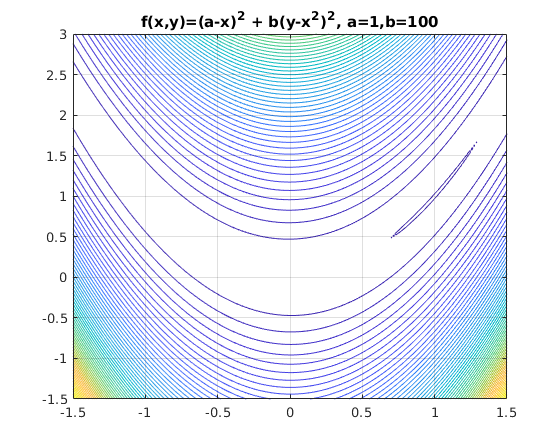
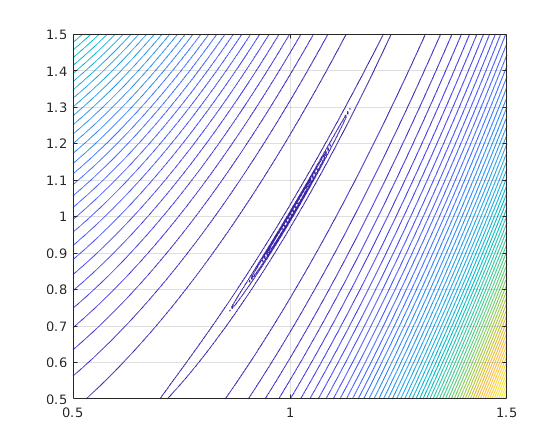
Contours closer to min pt.
figure x=linspace(0.5,1.5,200); y=linspace(0.5,1.5,200); [X,Y]=meshgrid(x,y); contour(x,y,f(X,Y),60) hold on contour(x,y,f(X,Y),[0,0.001 0.005 0.01 0.02 0.1]) grid on
Z=f(X,Y); min(Z(:))
ans = 6.3444e-04
Minimization algorithm: "brute force" vectorization
Domain: [-1.5,1.5]x[-1.5,3] (Previous figure,larger domain)
N=[200 400 800 1600]; Nlen=length(N); minpts=zeros(3,Nlen); T=zeros(1,Nlen); for k=1:Nlen tic x=linspace(-1.5,1.5,N(k)); y=linspace(-1.5,3,N(k)); %x=linspace(0.5,1.5,N(k));y=x; % tic [X,Y]=meshgrid(x,y); % tic Z=f(X,Y); % tic [minz,minind]=min(Z(:)); T(k)=toc; minpts(:,k)=[X(minind);Y(minind);minz]; end format long minpts format short T ratios=T(2:end)./T(1:end-1) % 2^nd run (First takes for setup etc., so run at least twice.) %{ T = 0.0065 0.0025 0.0089 0.0387 ratios = 0.3855 3.5368 4.3532 %}
minpts =
Columns 1 through 3
1.017587939698493 0.996240601503759 1.000625782227785
1.032663316582914 0.992481203007519 1.000625782227785
0.001105646701661 0.000014153051440 0.000039600970082
Column 4
1.000938086303940
1.001876172607880
0.000000880083355
T =
0.0009 0.0034 0.0095 0.0721
ratios =
3.6201 2.7881 7.5580
%{ figure x=linspace(-1.5,1.5,50); y=linspace(-1.5,3,50); [X,Y]=meshgrid(x,y); surf(x,y,f(X,Y)) %}
See how fminsearch handles Rosenbrock.
Repeat definitions:
a=1;b=100; f=@(x,y)(a-x).^2 + b*(y-x.^2).^2
f =
function_handle with value:
@(x,y)(a-x).^2+b*(y-x.^2).^2
Objective function must have intial point in the form of a vector.
Just like we had in part a):
fun = @(x) f(x(1),x(2));
One can set optional arguments with optimset (remember odeset)
opts=optimset('Display','iter-detailed'); opts.TolFun=1e-10; opts.TolX=1e-10; opts.MaxIter=200; opts.UseParallel=1; % Presumably doesn't do anything good as % algorithm is purely sequential. % opts.MaxFunEvals=1000;
Call fminsearch with opts set above
tic [x,fval]=fminsearch(fun,[-1 2],opts); TfminS=toc minptfminS=[x fval]
Iteration Func-count min f(x) Procedure
0 1 104
1 3 84.7531 initial simplex
2 5 45.8275 expand
3 7 13.1861 expand
4 9 4.98422 reflect
5 11 4.98422 contract outside
6 13 4.98422 contract inside
7 15 4.98422 contract inside
8 17 4.98422 contract inside
9 19 4.98422 contract outside
10 21 4.95047 reflect
11 23 4.91586 contract inside
12 25 4.83461 expand
13 27 4.83461 contract inside
14 29 4.72643 expand
15 31 4.64513 expand
16 33 4.34096 expand
17 34 4.34096 reflect
18 36 4.33543 reflect
19 38 3.94834 expand
20 39 3.94834 reflect
21 41 3.41421 expand
22 43 3.41421 contract inside
23 45 3.38899 reflect
24 47 2.94889 expand
25 49 2.94889 contract inside
26 51 2.46132 expand
27 53 2.46132 contract inside
28 54 2.46132 reflect
29 56 2.01407 expand
30 58 2.01407 contract inside
31 60 1.69086 expand
32 62 1.69086 contract inside
33 63 1.69086 reflect
34 65 1.60541 reflect
35 67 1.58097 contract inside
36 69 1.34218 expand
37 70 1.34218 reflect
38 72 1.16421 reflect
39 74 1.16421 contract inside
40 76 1.14734 reflect
41 78 1.0409 reflect
42 79 1.0409 reflect
43 81 0.965985 reflect
44 83 0.964565 contract inside
45 85 0.807119 expand
46 87 0.807119 contract inside
47 89 0.780114 reflect
48 91 0.627386 expand
49 93 0.627386 contract inside
50 95 0.524722 expand
51 96 0.524722 reflect
52 98 0.430904 reflect
53 99 0.430904 reflect
54 101 0.354952 reflect
55 103 0.354952 contract inside
56 104 0.354952 reflect
57 106 0.299383 reflect
58 108 0.299383 contract inside
59 110 0.284164 expand
60 112 0.196288 expand
61 113 0.196288 reflect
62 115 0.176495 reflect
63 117 0.161974 contract inside
64 119 0.133641 reflect
65 120 0.133641 reflect
66 122 0.102843 reflect
67 124 0.102843 contract inside
68 126 0.0958024 reflect
69 128 0.0805126 reflect
70 129 0.0805126 reflect
71 131 0.0642292 reflect
72 133 0.0642292 contract inside
73 135 0.0546237 expand
74 137 0.0370172 expand
75 139 0.0262263 expand
76 141 0.0160178 contract outside
77 143 0.0111434 reflect
78 145 0.00647626 contract outside
79 146 0.00647626 reflect
80 148 0.00511538 reflect
81 150 0.000642341 contract inside
82 151 0.000642341 reflect
83 153 0.000642341 contract outside
84 155 0.00027343 contract inside
85 157 1.38286e-05 contract inside
86 159 1.38286e-05 contract inside
87 160 1.38286e-05 reflect
88 162 1.38286e-05 contract inside
89 164 1.38286e-05 contract inside
90 166 1.24616e-05 contract inside
91 168 3.74388e-06 contract inside
92 170 3.28362e-07 contract inside
93 172 3.28362e-07 contract outside
94 174 3.28362e-07 contract inside
95 176 1.58552e-07 contract outside
96 178 1.24728e-07 contract inside
97 180 1.82164e-08 contract inside
98 182 1.82164e-08 contract inside
99 184 1.82164e-08 contract outside
100 186 4.85119e-09 contract inside
101 187 4.85119e-09 reflect
102 189 3.56011e-09 contract inside
103 191 1.81979e-09 contract inside
104 193 1.70617e-10 contract inside
105 195 1.70617e-10 contract inside
106 197 1.70617e-10 contract outside
107 199 1.70617e-10 contract inside
108 201 1.09453e-10 reflect
109 203 1.15336e-11 contract inside
110 205 1.15336e-11 contract inside
111 207 1.15336e-11 contract outside
112 209 6.32026e-12 contract inside
113 211 3.99753e-12 contract outside
114 213 2.09421e-12 contract inside
115 215 2.28767e-13 contract inside
116 217 2.28767e-13 contract outside
117 219 2.28767e-13 contract inside
118 220 2.28767e-13 reflect
119 222 5.14407e-14 contract inside
120 224 3.64399e-14 contract inside
121 226 3.24846e-14 contract inside
122 228 4.26621e-15 contract inside
123 230 4.26621e-15 contract inside
124 232 4.26621e-15 contract inside
125 233 4.26621e-15 reflect
126 235 4.73054e-16 contract inside
127 237 4.73054e-16 contract inside
128 239 4.73054e-16 contract inside
129 240 4.73054e-16 reflect
130 242 8.19386e-17 contract inside
131 244 8.19386e-17 contract inside
132 246 8.19386e-17 contract inside
133 248 6.52299e-17 reflect
134 250 3.31553e-18 contract inside
135 252 3.31553e-18 contract inside
136 254 3.31553e-18 contract outside
137 256 3.31553e-18 contract inside
138 258 9.24237e-19 contract outside
139 260 4.04e-19 contract inside
140 262 4.04e-19 contract inside
141 264 2.05218e-19 contract inside
142 266 5.45955e-20 contract inside
143 268 5.45955e-20 contract inside
144 270 1.27595e-20 contract outside
145 272 7.55893e-21 contract inside
146 274 6.78047e-21 contract inside
147 276 1.91179e-21 contract inside
148 278 8.22208e-22 contract inside
149 280 8.05076e-22 contract inside
Optimization terminated:
the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-10
and F(X) satisfies the convergence criteria using OPTIONS.TolFun of 1.000000e-10
TfminS =
0.0305
minptfminS =
1.0000 1.0000 0.0000
opts.Display % Iterations: 149 % Accuracy great, because: opts.TolFun opts.TolX
ans =
'iter-detailed'
ans =
1.0000e-10
ans =
1.0000e-10
Timing: Slower than simple vector-min