Apollosolution.m
15.3.2018 HA
Contents
- Plot of orbit
- Text to plots (start with gtext, then change to text)
- Adjust tolerances:
- New options - New figure
- Compute "periodicity error"
- Next animate: (Skip now)
- For fun: animate the rays from earth to orbit.
- Look at stepsizes
- More precise computaion with logical indexing etc. (skip here)
- How close does the Apollo come to the surface of the earth?
- Find the minimum of
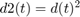
- Mark min distance point to figure(2)
- Use logical indexing
- More fun:
close all
type Apollosys
function [du] = Apollosys(t,u)
mu=1/82.45; % Ratio of masses: M_moon/M_earth;
lam=1-mu;
% Auxiliary variables:
% x=u1,x'=u2,y=u3,y'=u4
% For convenience take local variables:
u1=u(1);u2=u(2);u3=u(3);u4=u(4);
r1=sqrt((u1+mu).^2 + u3.^2);
r2=sqrt((u1-lam).^2 + u3.^2);
% Note: all variables are scalars => no need for .^ (works though).
du=[u2;
2*u4+u1-lam*(u1+mu)./r1.^3-mu*(u1-lam)./r2.^3;
u4;
-2*u2+u3-lam*u3./r1.^3-mu*u3./r2.^3];
end
mu=1/82.45; % Note: These values don't pass to the function Apollosys lam=1-mu; u0=[1.2; 0; 0; -1.04935751]; % x(0);x'(0);y(0);y'(0) %u0=[1.2;0;0;-0.9]; % Another set of initial values, try your own! Tperiod=6.19217; % Given value for period. %tmax=4*pi; % Longer ... %tmax=2; % or shorter T-ranges Tspan=[0 Tperiod]; [T,U]=ode45(@Apollosys,Tspan,u0);
Plot of orbit
figure
x=U(:,1); y=U(:,3); % Orbit
plot(x,y);shg
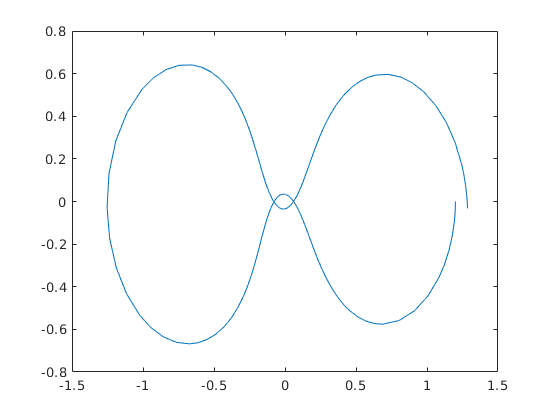
hold on plot(u0(1),u0(3),'*b') % Initial point. (b=blue) % plot(x(1),y(1),'*b') % Same as the previous line. plot(x(end),y(end),'ko') % Final point (k=black) plot(-mu,0,'*k',lam,0,'or') % plot earth and moon (r=red) %legend('Orbit','Initial pt.','Final pt.','Earth','Moon') grid on
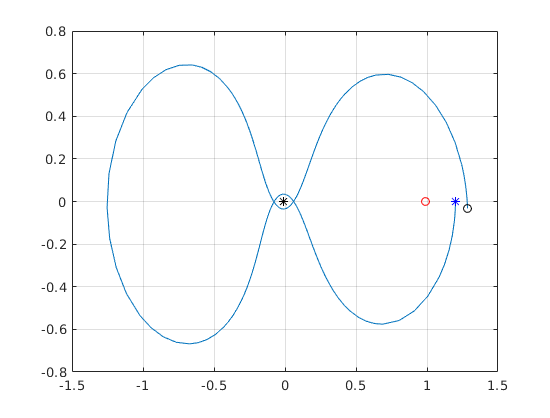
Text to plots (start with gtext, then change to text)
%gtext('Earth') % Get text coordinates with mouse. text(-.2,-.1,'Earth') % gtext('Moon') text(.77,-.1,'Moon') title('Restricted 3-body, default tolerances')
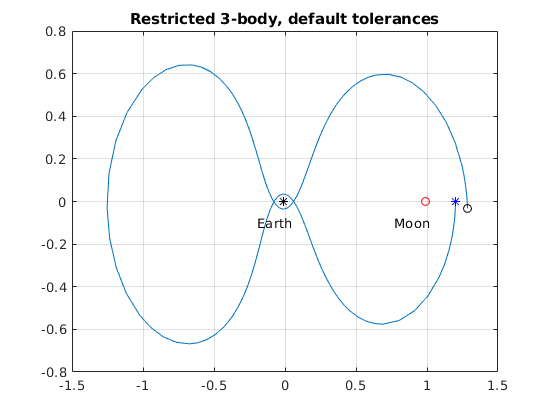
Adjust tolerances:
options=odeset('AbsTol',1e-6,'RelTol',1e-8); options.Stats='on'; options [T1,U1]=ode45(@Apollosys,Tspan,u0,options);
options =
struct with fields:
AbsTol: 1.0000e-06
BDF: []
Events: []
InitialStep: []
Jacobian: []
JConstant: []
JPattern: []
Mass: []
MassSingular: []
MaxOrder: []
MaxStep: []
NonNegative: []
NormControl: []
OutputFcn: []
OutputSel: []
Refine: []
RelTol: 1.0000e-08
Stats: 'on'
Vectorized: []
MStateDependence: []
MvPattern: []
InitialSlope: []
163 successful steps
15 failed attempts
1069 function evaluations
New options - New figure
figure; clf hold on plot(U1(:,1),U1(:,3));shg % Orbit: x=U1(:,1); y=U1(:,3); plot(u0(1),u0(3),'*b') % Initial point. % plot(U1(1,1),U1(1,3),'*') % Same as the previous line. plot(U1(end,1),U1(end,3),'ko') % Final point % Now is periodic at the accuracy of pic. plot(-mu,0,'*k',lam,0,'or') % plot earth and moon title('Restricted 3-body, new tolerances') %legend('Orbit','Initial pt.','Final pt.','Earth','Moon') grid on
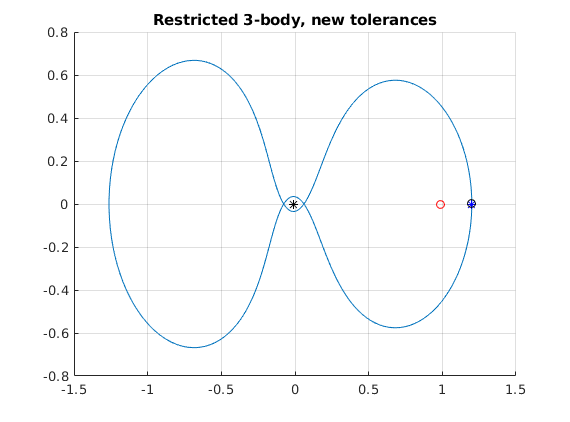
Smaller tolerances ==> Periodicity is shown at the accuracy of graphics.
Compute "periodicity error"
x1=U1(:,1);y1=U1(:,3); deltax=x1(1)-x1(end); deltay=y1(1)-y1(end); dist=sqrt(deltax^2+deltay^2) % Distance from initial point to final pt. relerr=dist/x1(1) % Relative error % 6.3511e-06 % So Periodic with about 6 numbers of accuracy. %
dist = 7.6214e-06 relerr = 6.3511e-06
Next animate: (Skip now)
The simplest way for animation. For publish, comment this away
%{ figure axis([-1.5 1.5 -.8 .8]); hold on grid on for j=1:length(T1) plot(x1(j),y1(j),'.r','MarkerSize',4) pause(0.01) % adjust end %} % Don't need for-loop for "still" picture, just: % plot(x1,y1,'or','MarkerSize',4) % The "still" picture command ... % % to be "decommented" for publish %
For fun: animate the rays from earth to orbit.
(Remove comments if you like)
%{ for j=1:length(T1) plot([0 x1(j)],[0 y1(j)],'k') pause(0.005) % adjust end %}
Look at stepsizes
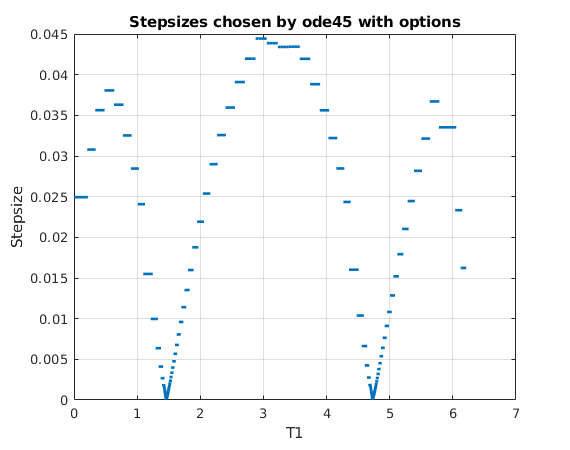
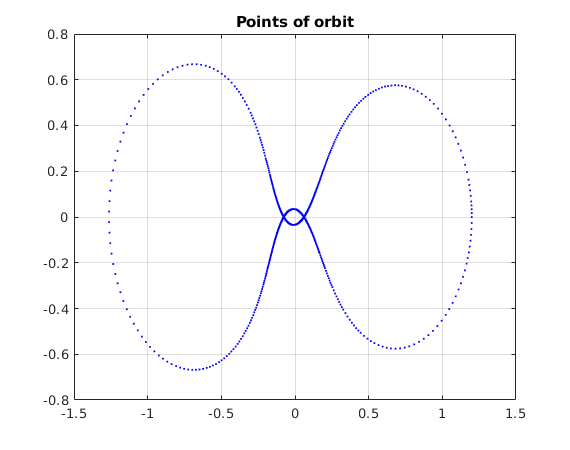
figure % % diff(T1) gives the difference vector: % (T1(2)-T1(1),T1(3)-T1(2),...,T1(end)-T1(end-1)) % length=length(T1)-1 plot(T1(2:end),diff(T1),'.');grid on;shg xlabel('T1') ylabel('Stepsize') title('Stepsizes chosen by ode45 with options') figure plot(x1,y1,'.b','MarkerSize',4) title('Points of orbit') grid on % Zoom in to see that step sizes stay the same for a few steps usually. % From the figure we see that the min and max stepsizes occur about at: % t=1.5 and t=4.8 (min) and t=0.5, 3, 5.7 (max) %
More precise computaion with logical indexing etc. (skip here)
Do along ideas outlined in the commented block.
%{ [min1,ind1]=min(steps) t1=T((T>1)&(T<3)) steps1=steps((T>1)&(T<3)); [min2,ind2]=min(steps1) t2=t1(ind2) hold on plot(U1(ind2,1),U1(ind2,3),'*r') %}
How close does the Apollo come to the surface of the earth?
Real sizes in kilometers:
distMoonEarth = 384400; R_earth= 6371; R_moon = 1737;
Distance to centre:
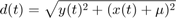
Find the minimum of 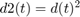
x=U1(:,1); y=U1(:,3); D2=y.^2+(x+mu).^2; [minval2,minind]=min(D2); % Finds the first minimum and its index. xmin=x(minind); ymin=y(minind); minpoint=[xmin ymin] minD=sqrt(minval2); minDreal=minD*distMoonEarth dist_to_surface_earth=minDreal-R_earth %
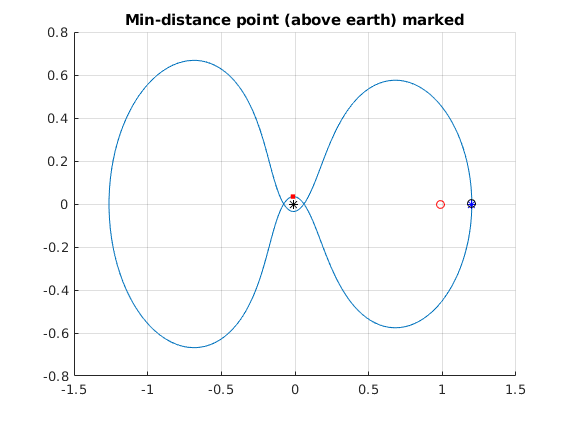
minpoint = -0.0140 0.0346 minDreal = 1.3317e+04 dist_to_surface_earth = 6.9458e+03
Mark min distance point to figure(2)
figure(2) hold on plot(xmin,ymin,'.r','MarkerSize',10) title('Min-distance point (above earth) marked')
Use logical indexing
Skip this part now.
%{ D2=@(x,y)y.^2+(x+mu).^2; % Define D2 as a function handle. minval2=min(D2(x,y)) ind=D2(x,y)==minval2; sum(ind) %}
More fun:
ApollosolutionInteractive.m Interactive choice of initial points (like in dirfields earlier in the course)
Mathworks demo: orbitode contains advanced Matlab techniques, s.k. events. That gives a way to control the Timespan for various trajectories.